حلول الأسئلة
السؤال
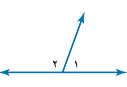
اكتب معادلة تمثل مجموع ق![]() ١ و ق
١ و ق ![]() ٢ ومعادلة أخرى تمثل مجموع ق
٢ ومعادلة أخرى تمثل مجموع ق![]() ٢ و ق
٢ و ق![]() ٣.
٣.
الحل
مجموع ق U ١ +ق U ٢ = ١٨٠
١
مجموع ق U ٢+ U ٣ = ١٨٠
٢
شاهد حلول جميع الاسئلة
حل اسئلة تدرب وحل المسائل
حدد ما إذا كان كل زوج من الزوايا الآتية متكاملة أو متتامة أو غير ذلك.
٤) .JPG)
مجموع الزاويتان = ٩٠ + ٤٣ = ١٣٣°
إذاً الزاويتان غير متتامتان وغير متكاملتان.
٥) .JPG)
مجموع الزاويتان = ٦١ + ١١٩ = ١٨٠°
إذاً الزاويتان متكاملتان.
٦) .JPG)
مجموع الزاويتان = ٩٠ + ٩٠ = ١٨٠°
إذا الزاويتان متكاملتان.
٧) .JPG)
بما أن مجموع الزاويتان ١٨٠°
إذاً الزاويتان متكاملتان.
٨) .JPG)
بما أن مجموع الزاويتان ٩٠°
إذاً الزاويتان متتامتان.
٩) .JPG)
بما أن مجموع الزاويتان أكبر من ٩٠° وأقل من ١٨٠°
إذاً الزاويتان غير متكاملتان وغير متتامتان.
١٠) جبر: إذا كانت ![]() أ و
أ و ![]() ب متتامتين، وكان ق
ب متتامتين، وكان ق![]() ب يساوي ٦٧° فما ق
ب يساوي ٦٧° فما ق![]() أ؟
أ؟
بما أن U أ و U ب متتامتان، ق U ب = ٦٧°
إذاً U أ + U ب = ٩٠°
U أ + ٦٧° = ٩٠°
U أ = ٢٣°
١١) جبر: أوجد ق![]() ج إذا كانت
ج إذا كانت ![]() ج و
ج و ![]() د متكاملتان، وكان ق
د متكاملتان، وكان ق![]() د يساوي ١١٥°.
د يساوي ١١٥°.
بما أن U ج و U د متكاملتان، ق U د = ١١٥°
إذاً U ج + U د = ١٨٠°
U ج + ١١٥ = ١٨٠ اطرح ١١٥ من الطرفين.
U ج = ٦٥°
١٢) أدوات مدرسية: ما قياس الزاوية المجاورة في الشكل المجاور؟
بما أن الزاويتين تصنعان زاوية مستقيمة، مجموع الزاويتان = ١٨٠°
١١٦ + س = ١٨٠° اطرح ١١٦ من الطرفين.
س = ٦٤°
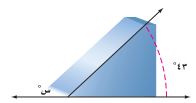
١٣) لوح التزلج: تشكل قاعدة التزلج في الشكل المجاور زاوية قياسها ٤٣° أوجد قياس الزاوية المجهولة.
الزاويتان متكاملتان أي مجموعهما ١٨٠°
٤٣ + س = ١٨٠ اطرح ٤٣ من الطرفين.
س = ١٣٧°
استعمل الشكل المجاور للإجابة عن الأسئلة ١٤ - ١٦.
١٤) سم زوجاً من الزوايا المتتامّة.
U ج ر ك و U ك ر ي.
١٥) سم زوجاً من الزوايا المتكاملة.
U ج ر د و U ج ر ي.
١٦) سم زوجاً من الزوايا المتقابلة بالرأس.
U ب ك أ وU ر ك ي.
هندسة: استعمل الشكل المجاور للإجابة عن الأسئلة ١٧ - ٢٠.
١٧) حدد ما إذا كان كل زوج من الزوايا ![]() ١ و
١ و ![]() ٢،
٢، ![]() ٢ و
٢ و ![]() ٣،
٣، ![]() ١ و
١ و ![]() ٣ يمثل زاويتين متقابلتين بالرأس أو متجاورتين أو غير ذلك.
٣ يمثل زاويتين متقابلتين بالرأس أو متجاورتين أو غير ذلك.
U ١ وU ٢ متجاورتين.
U ٢ وU ٣ متجاورتين.
U ٢ وU ٣ متقابلتين بالرأس.
١٨) اكتب معادلة تمثل مجموع ق![]() ١ و ق
١ و ق ![]() ٢ ومعادلة أخرى تمثل مجموع ق
٢ ومعادلة أخرى تمثل مجموع ق![]() ٢ و ق
٢ و ق![]() ٣.
٣.
مجموع ق U ١ +ق U ٢ = ١٨٠° ١
مجموع ق U ٢+ U ٣ = ١٨٠° ٢
١٩) حل المعادلتين اللتين كتبتهما في السؤال ١٨ لحساب ق![]() ١، و ق
١، و ق![]() ٣ على الترتيب بدلالة ق
٣ على الترتيب بدلالة ق![]() ٢. ما الذي تلاحظه؟
٢. ما الذي تلاحظه؟
U ١ = ١٨٠ - U ٢ ٣
U ٣ = ١٨٠ - U ٢
ألاحظ أن المعادلتين متماثلتين.
٢٠) خمن: استعن بإجابتك في السؤال ١٩ لتخمين العلاقة بين الزوايا المتقابلة بالرأس.
استنتج أن الزوايا المتقابلة بالرأس متساوية.
أوجد قيمة س في كل من الأشكال الآتية:
٢١) .JPG)
بما أن الزاويتين متقابلتين بالرأس، إذا متساويتين،
س = ٤٠°
٢٢) .JPG)
بما أن الزاويتين متتامتين، مجموعهما = ٩٠°
س = ٩٠ - ٣٥ = ٥٥°
٢٣) .JPG)
بما أن الزاويتين متكاملتين، مجموعهما = ١٨٠°
س = ١٨٠ - ٢٠ = ١٦٠°
٢٤) اختيار من متعدد: مستعيناً بالشكل المجاور، أي الجمل الآتية صحيحة؟
أ) ١ و
٢ متكاملتان.
ب) ١ و
٢ متقابلتان بالرأس
جـ) ١ و
٢ متتامتان.
د) ١ و
٢ قائمتان.
الجملة الصحيحة أ) U ١ وU ٢ متكاملتان.


.JPG)

.JPG)
.JPG)