وضح إذا كانت العبارة "يمكن استعمال التوزيع بالترتيب لضرب ثنائية حد ثلاثية حدود" صحيحة دائماً، أم صحيحة أحياناً، أم غير صحيحة أبداً، وفسر إجابتك.

صحيحة دائماً، يمكنك تجميع كل حدين متجاورين في ثلاثية الحدود ثم تتعامل مع ثلاثية الحدود كمجموع عبارتين وتطبق عليهما طريقة التوزيع بالرتيب.

حل أسئلة تدرب وحل المسائل

أوجد ناتج الضرب في كل مما يأتي:

١٠) (٥ص - ٤) (٣ص - ١)

المقدار = ٥ص(٣ص) + ٥ص (-١) + (-٤) (٣ص) + (-٤) (-١)

= ١٥ص^٢ - ٥ص - ١٢ص + ٤

= ١٥ص^٢ - ١٧ص + ٤

١١) (٦د - ٥) (٤د - ٧)

المقدار = ٦د(٤د) + ٦د (-٧) + (-٥) (٤د) + (-٥) (-٧)

= ٢٤د^٢ - ٤٢د - ٢٠د + ٣٥

= ٢٤د^٢ - ٦٢د + ٣٥

١٢) (٣م + ٥) (٢م + ٣)

المقدار = ٣م(٢م) + ٣م (٣) + ٥(٢م) + ٥(٣)

= ٦م^٢ + ٩م + ١٠م + ١٥

= ٦م^٢ + ١٩م + ١٥

١٣) (١٢ن - ٥) (١٢ن + ٥)

المقدار = ١٢ن(١٢ن) + ١٢ن (٥) + (-٥) (١٢ن) + (-٥) (٥)

= ١٤٤ن^٢ + ٦٠ن -٦٠ن - ٢٥

= ١٤٤ن^٢ - ٢٥

١٤) (٥ر + ٧) (٥ر - ٧)

$$\begin{gathered} \mathrm{٥}ر + \mathrm{٧} \\ \underline{ر \times \mathrm{٥} - \mathrm{٧}} \\ \mathrm{٢٥} {ر}^{\mathrm{٢}} -\mathrm{٣٥} ر \\ \underline{ \mathrm{٣٥} ر -\mathrm{٤٩}} \\ \mathrm{٢٥} {ر}^{\mathrm{٢}} -\mathrm{٤٩} \end{gathered}$$

المقدار = ٢٥ر^٢ - ٤٩

١٥) (٨ل + ٤س) (٥ل - ٦س)

= ٨ل(٥ل) + ٨ل(-٦س) + ٤س(٥ل) + ٤س(-٦س)

= ٤٠ل^٢ + ٤٨س + ٢٠ ل س - ٢٤س^٢

= ٤٠ل^٢- ٢٨ل س - ٢٤س^٢

١٦) حديقة: يحيط ممر عرضه س بحديقة مستطيلة الشكل، ٨ أمتار، وعرضها ٦ أمتار، اكتب عبارة تمثل المساحة الكلية للحديقة والممر.

المساحة الكلية = (طول الحديقة + ٢الممر) (عرض الحديقة + ٢الممر).

المساحة الكلية = (٢س + ٦) × (٢س + ٨)

= ٤س^٢ + ١٦س + ١٢س + ٤٨

= ٤س^٢ + ٢٨س + ٤٨

أوجد ناتج الضرب في كل مما يأتي:

١٧) (٢ص - ١١) (ص^٢ - ٣ص + ٢)

$$\begin{gathered} ص -\mathrm{٣} ص + \mathrm{٢} \\ \underline{ص \times \mathrm{٢} - \mathrm{١١}} \\ \mathrm{٢} {ص}^{\mathrm{٣}} - \mathrm{٦} {ص}^{\mathrm{٢}} + \mathrm{٤} ص \\ \underline{ -\mathrm{١١}{ص}^{\mathrm{٢}} + \mathrm{٣٣}ص - \mathrm{٢٢}} \\ \mathrm{٢} {ص}^{\mathrm{٣}} - \mathrm{١٧}{ص}^{\mathrm{٢}} + \mathrm{٣٧}ص - \mathrm{٢٢} \end{gathered}$$

المقدار = ٢ص^٣ - ١٧ص^٢ + ٣٧ص - ٢٢

١٨) (٤أ + ٧) (٩أ + ٢أ - ٧)

$$\begin{gathered} \mathrm{٩}أ +\mathrm{٢}أ - \mathrm{٧} \\ \underline{\times \mathrm{٤} + \mathrm{٧}} \\ \mathrm{٣٦}{أ}^{\mathrm{٣}} + \mathrm{٨}{أ}^{\mathrm{٢}} - \mathrm{٢٨}أ \\ \underline{ + \mathrm{٦٣}{أ}^{\mathrm{٢}} + \mathrm{١٤}أ - \mathrm{٤٩}} \\ \mathrm{٣٦}{أ}^{\mathrm{٣}} + \mathrm{٧١}{أ}^{\mathrm{٢}} - \mathrm{١٤}أ - \mathrm{٤٩} \end{gathered}$$

المقدار = ٣٦أ^٣ + ٧١أ^٢ - ١٤أ - ٤٩

١٩) (س^٢ + ٥س - ١) (٥س^٢ - ٦س + ١)

$$\begin{gathered} س +\mathrm{٥}س - \mathrm{١} \\ \underline{س\times \mathrm{٥}س - \mathrm{٦} + \mathrm{١}} \\ \mathrm{٥}{س}^{\mathrm{٤}} + \mathrm{٢٥}{س}^{\mathrm{٣}} - \mathrm{٥}{س}^{\mathrm{٢}} \\ -\mathrm{٦}{س}^{\mathrm{٣}} -\mathrm{٣٠}{س}^{\mathrm{٢}} +\mathrm{٦}س \\ \underline{ {س}^{\mathrm{٢}} +\mathrm{٥}س - \mathrm{١} } \\ \mathrm{٥}{س}^{\mathrm{٤}} + \mathrm{١٩}{س}^{\mathrm{٣}} - \mathrm{٣٤}{س}^{\mathrm{٢}} + \mathrm{١١}س - \mathrm{١} \end{gathered}$$

المقدار = ٥س^٤ + ١٩س^٣ -٣٤س^٢ + ١١س - ١

٢٠) (٦ع^٢ - ٥ع - ٢) (٣ع^٣ - ٢ع - ٤)

$$\begin{gathered} \mathrm{٦}{ع}^{\mathrm{٢}} - \mathrm{٥}ع - \mathrm{٢} \\ \times \underline{\mathrm{٣}{ع}^{\mathrm{٣}} - \mathrm{٢}ع -\mathrm{٤}} \\ \mathrm{١٨}{ع}^{\mathrm{٥}} - \mathrm{١٥}{ع}^{\mathrm{٤}} - \mathrm{٦}{ع}^{\mathrm{٣}} \\ -\mathrm{١٢}{ع}^{\mathrm{٣}} + \mathrm{١٠}{ع}^{\mathrm{٢}} + \mathrm{٤}ع \\ \underline{ -\mathrm{٢٤}ع + \mathrm{٢٠}ع + \mathrm{٨}} \\ \mathrm{١٨}{ع}^{\mathrm{٥}} - \mathrm{١٥}{ع}^{\mathrm{٤}} - \mathrm{١٨}{ع}^{\mathrm{٣}} -\mathrm{١٤}{ع}^{\mathrm{٢}} + \mathrm{٢٤}ع + \mathrm{٨} \end{gathered}$$

المقدار = ١٨ع^٥ - ١٥ع^٤ - ١٨ع^٣ - ١٤ع^٢ - ٢٤ع + ٨

٢١) بسط العبارة: (م + ٢) [(م^٢ + ٣م - ٦) + (م^٢ - ٢م + ٤)]

المقدار = (م + ٢) (م^٢ + ٣م - ٦ + م^٢ - ٢م + ٤)

= (م + ٢) (٢م^٢ + م - ٢)

$$\begin{gathered} \mathrm{٢}{م}^{\mathrm{٢}} + م - \mathrm{٢} \\ \underline{\times +\mathrm{٢}} \\ \mathrm{٢}{م}^{\mathrm{٣}} + م -\mathrm{٢}م \\ \underline{ \mathrm{٤}م + \mathrm{٢}م - \mathrm{٤}} \\ \mathrm{٢}{م}^{\mathrm{٣}} + \mathrm{٥}{م}^{\mathrm{٢}} -\mathrm{٤} \end{gathered}$$

المقدار = ٢م^٣ + ٥م^٢ - ٤

هندسة: اكتب عبارة تمثل مساحة كل منطقة مظللة مما يأتي:

٢٢)

• مساحة الدائرة = ط نق^٢

= ط (٢س + ٣)^٢ = ٤ط س + ١٢ س ط + ٩ط

• مساحة المستطيل = الطول × العرض.

= (س+ ١) (٣س + ٢)

= ٣س^٢ + ٢س + ٣س + ٢

= ٣س + ٥س + ٢

• مساحة الشكل المظلل = مساحة الدائرة - مساحة المستطيل.

= (٤ط س^٢ + ١٢س ط + ٩ط) - (٣س^٢ + ٥س + ٢)

= ٤ط س^٢ + ١٢ط س + ٩ط - ٣س^٢ - ٥س - ٢

٢٣)

• مساحة المثلث = $\frac{\mathrm{١}}{\mathrm{٢}}$ القاعدة × الارتفاع.

= $\frac{\mathrm{١}}{\mathrm{٢}}$(٢س - ٣) × (٤س + ١)

= $\frac{\mathrm{١}}{\mathrm{٢}}$(٨س^٢ + ٢س - ١٢س - ٣)

= ٤س^٢ - ٥س - $\frac{\mathrm{٣}}{\mathrm{٢}}$

• مساحة المستطيل = الطول × العرض.

= ٥س × (٤س + ١)

= ٢٠س^٢ + ٥س

• مساحة الشكل المظلل = مساحة المثلث + مساحة المستطيل.

= ٤س^٢ - ٥س - $\frac{\mathrm{٣}}{\mathrm{٢}}$ + ٢٠س^٢ + ٥س

= ٢٤س^٢ + $\frac{\mathrm{٣}}{\mathrm{٢}}$

٢٤) كرة طائرة: تمثل العبارتان: (٧ص - ٥) متر، (٨ص + ٢) متر بعدي ملعب كرة طائرة.

أ) اكتب عبارة تمثل مساحة الملعب.

مساحة الملعب = الطول × العرض.

مساحة الملعب = (٧ص - ٥) × (٨ص + ٢)

= ٥٦ص^٢ + ١٤ص - ٤٠ص - ١٠

= ٥٦ص^٢ - ٢٦ص - ١٠

ب) إذا كان طول ملعب كرة طائرة ١٨م، فأوجد مساحته.

طول الملعب = ٨ص + ٢

٨ص + ٢ = ١٨

٨ص = ١٦

ص = ٢

مساحة الملعب = ٥٦ص^٢ - ٢٦ص - ١٠

= ٥٦(٢)^٢ - ٢٦ × ٢ - ١٠

= ١٦٢ م^٢

٢٥) هندسة: اكتب عبارة تمثل مساحة مثلث طول قاعدته ٢س + ٣، وارتفاعه ٣س - ١

مساحة المثلث = $\frac{\mathrm{١}}{\mathrm{٢}}$ طول القاعدة × الارتفاع.

= $\frac{\mathrm{١}}{\mathrm{٢}}$(٢س + ٣) × (٣س - ١)

= $\frac{\mathrm{١}}{\mathrm{٢}}$(٦س^٢ - ٢س + ٩س - ٣)

= $\frac{\mathrm{١}}{\mathrm{٢}}$(٦س + ٧س - ٣)

= ٣س + $\frac{\mathrm{٧}}{\mathrm{٢}}$س - $\frac{\mathrm{٣}}{\mathrm{٢}}$

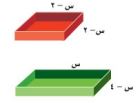
٢٦) قوالب: تسمح القوالب المختلفة بصنع ألواح شوكولاتة مربعة أو مستطيلة الشكل كما هو مبين جانباً.

أ) ما قيم س الممكنة؟ فسر إجابتك.

س > ٤، إذا كانت س = ٤

فإن عرض الصندوق سيصبح صفراً

س < ٤، فإن عرض الصندوق سيصبح سالباً.

ب) أي الشكلين مساحته أكبر؟

مساحة المربع = (س - ٢)^٢ = س^٢ - ٢س + ٤

مساحة المستطيل = س (س - ٤) = س^٢ - ٤س

بفرض = ٥

مساحة المربع = ٢٥ - (٢ × ٥) + ٤ = ١٩ وحدة.

مساحة المستطيل = ٢٥ - (٤ × ٥) = ٥ وحدات.

المساحة الأكبر هي المربع.

جـ) ما الفرق بين مساحتي القالبين؟

الفرق = (س - ٢) - س (س - ٤)

= س^٢ + ٤ - ٤س - س^٢ + ٤س

= ٤ سم٢

٢٧) تمثيلات متعددة: ستكتشف في هذا السؤال قاعدة مربع مجموع حدين.

أ) جدولياً: انقل الجدول الآتي وأكمله.

ب) لفظياً: اكتب جملة توضح كيفية الحصول على مربع مجموع حدين.

• أول حد في مربع مجموع حدين، هو مربع الحد الأول.
• والحد الأوسط، هو مثلي حاصل ضرب الأول بالحد الثاني.
• والحد الثالث، هو مربع الحد الثاني.

جـ) رمزياً: اكتب عبارة تمثل مربع مجموع الحدين أ + ب.

(أ + ب)^٢ = أ(أ) + أب + أب + ب^٢

= أ^٢ + ٢أب + ب^٢

٢٨) تبرير: وضح إذا كانت العبارة "يمكن استعمال التوزيع بالترتيب لضرب ثنائية حد ثلاثية حدود" صحيحة دائماً، أم صحيحة أحياناً، أم غير صحيحة أبداً، وفسر إجابتك.

صحيحة دائماً، يمكنك تجميع كل حدين متجاورين في ثلاثية الحدود ثم تتعامل مع ثلاثية الحدود كمجموع عبارتين وتطبق عليهما طريقة التوزيع بالرتيب.

٢٩) تحد: أوجد ناتج: (س ^م + س ^ن) (س ^م-١ - س ^١-ن + س ^ن)

المقدار = س ^م(س ^م-١) + س ^م(- س^١-ن) + س ^م(س ^ن) + س ^ن(س ^م-١) + س ^ن(- س^١-ن) + س ^ن(س ^ن)

= س ^م+م-١ - س ^م+١-ن + س ^م+ن + س ^م-١+ن - س ^ن+١-ن + س^٢ن

= س^٢م-١ - س ^م-ن+١ + س ^م+ن + س ^م+ن-١ - س + س^٢ن

٣٠) مسألة مفتوحة: اكتب ثنائية وثلاثية حدود تتضمن كل منهما متغيراً واحداً، ثم أوجد ناتج ضربهما.

س - ١، س^٢ - س - ١

(س - ١) (س^٢ - س - ١) = س^٣ - ٢س^٢ + ١

٣١) اكتب: لخص الطرق التي يمكن استعمالها لضرب كثيرات الحدود.

يمكن استعمال الضرب رأسياً وذلك بتوزيع الضرب وتجميع الحدود وتستعمل طريقة التوزيع بالترتيب أو الطريقة الأفقية حيث تضرب كلا من الحدين.

٣٢) ما ناتج ضرب العبارتين: ٢س - ٥، ٣س + ٤؟

أ) ٥س - ١

ب) ٦س^٢ -٧س - ٢٠

جـ) ٦س^٢ - ٢٠

د) ٦س^٢ + ٧س - ٢٠

(٢س - ٥) × (٣س + ٤) = ٦س^٢ + ٨س - ٥(٣س) - ٢٠

= ٦س^٢ + ٨س - ١٥س - ٢٠

= ٦س^٢ + ٧س - ٢٠

إذن الإجابة ب) ٦س^٢ + ٧س - ٢٠

٣٣) إجابة قصيرة: أي نقطة على خط الأعداد تمثل عدداً مكعبة أكبر منه؟

النقطة ن.