أوجد المساحة الجانبية والكلية لسطح كل هرم منتظم مما يأتي مقرباً الجواب إل أقرب جزء من عشرة إذا لزم الأمر.

المساحة الجانبية للهرم = $\frac{\mathrm{١}}{\mathrm{٢}}$ مح × ل

المساحة الجانبية للهرم = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٢ (١,٧٥+ ١,٧٥) × ٢ = ٧

المساحة الكلية للهرم = المساحة الجانبية + مساحة القاعدة.

المساحة الكلية للهرم = ٧ + (١,٧٥ + ١,٧٥) = ١٠,١

حل أسئلة مراجعة تراكمية

٦٥- أوجد مساحة المنطقة المظللة في الشكل المجاور مقرباً الجواب إلى أقرب جزء من عشرة.

مساحة المستطيل = الطول × العرض = ٥ × ١٠ = ٥٠

مساحة الدائرة = ط نق^٢ = ط (٢,٥)^٢ = ١٩,٦

مساحة المنطقة المظللة = مساحة المستطيل - مساحة الدائرة.

مساحة المنطقة المظللة = ٥٠ - ١٩,٦ = ٣٠,٤ م^٢

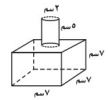
٦٦- أوجد المساحة الجانبية والكلية للمجسم المجاور مقرباً الجواب إلى أقرب جزء من عشرة.

• المساحة الجانبية = محيط القاعدة × الارتفاع

المساحة الجانبية = (٧+ ٧) × ٢×٧ = ١٩٦

• المساحة الكلية = المساحة الجانبية + مساحة القاعدتين

المساحة الكلية = ١٩٦ + ٢(٧×٧) = ٢٩٤

• المساحة الجانبية للأسطوانة = محيط القاعدة × الارتفاع

المساحة الجانبية = ٢ ط نق× ع = ٢ ط × ٥ = ٣١,٤

• المساحة الكلية = المساحة الجانبية + مساحة القاعدتين

المساحة الكلية = ٣١,٤ + ٢ ط = ٣٧,٧

أوجد المساحة الجانبية والكلية لسطح كل هرم منتظم مما يأتي مقرباً الجواب إل أقرب جزء من عشرة إذا لزم الأمر.

٦٧-

• المساحة الجانبية للهرم = $\frac{\mathrm{١}}{\mathrm{٢}}$ مح × ل

المساحة الجانبية للهرم = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٢٧ × ١٠,٢ = ١٣٧,٧

• المساحة الكلية للهرم = المساحة الجانبية + مساحة القاعدة

المساحة الكلية للهرم = ١٣٧,٧ + $\frac{\mathrm{١}}{\mathrm{٢}}$ (٧,٨ × ٩) = ١٧٢,٨

٦٨-

• المساحة الجانبية للهرم = $\frac{\mathrm{١}}{\mathrm{٢}}$ مح × ل

المساحة الجانبية للهرم = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٢ (١,٧٥+ ١,٧٥) × ٢ = ٧

• المساحة الكلية للهرم = المساحة الجانبية + مساحة القاعدة

المساحة الكلية للهرم = ٧ + (١,٧٥ + ١,٧٥) = ١٠,١

٦٩-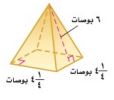

• المساحة الجانبية للهرم = $\frac{\mathrm{١}}{\mathrm{٢}}$ مح × ل

المساحة الجانبية للهرم = $\frac{\mathrm{١}}{\mathrm{٢}}$ × ٢($\frac{\mathrm{١}}{\mathrm{٤}}\mathrm{٤}+\frac{\mathrm{١}}{\mathrm{٤}}\mathrm{٤}$) × ٦ = ٥١

• المساحة الكلية للهرم = المساحة الجانبية + مساحة القاعدة

المساحة الكلية للهرم = ٥١ + ($\frac{\mathrm{١}}{\mathrm{٤}}\mathrm{١}\times \frac{\mathrm{١}}{\mathrm{٤}}\mathrm{١}$) = ٥٢,٦

مهارة سابقة: حل كل معادلة مما يأتي ثم تحقق من صحة الحل:

٧٠- س + ٨ = ٢

س + ٨ = ٢

س = ٢ - ٨

س = -٦

للتحقق من صحة الحل: -٦ +٨ = ٢

٢=٢ C

٧١- ص - ٥ = -٩

ص - ٥ = -٩

ص = -٩ + ٥

ص = -٤

للتحقق من صحة الحل:

-٤ -٥ = -٩

-٩ = -٩ C

٧٢- ٣٢ = -٤ن

-٣٢ = -٤ن

ن = $\frac{\mathrm{٣٢}}{-\mathrm{٤}}$ = -٨

للتحقق من صحة الحل:

٣٢ = -٤ × -٨

٣٢ = ٣٢ C

٧٣- $\frac{\mathrm{١}}{\mathrm{٣}}$ = -١٥

أ = -١٥ × ٣

أ = -٤٥

للتحقق من صحة الحل:

$\frac{-\mathrm{٤٥}}{\mathrm{٣}}=-\mathrm{١٥}$

-١٥ = -١٥ C