اكتب برهاناً إحداثياً للعبارة الآتية: إذا كان الشكل الرباعي متوازي أضلاع فإن قطريه ينصف كل منهما الآخر.

المعطيات: ABCD متوازي أضلاع.

المطلوب: $\overline{AC}$ و $\overline{DB}$ ينصف كل منهما الآخر.

البرهان:

نقطة منتصف $\overline{AC}$

$\begin{array}{r}\left(\frac{a+b}{2},\frac{c}{2}\right)=\left(\frac{0+(a+b)}{2},\frac{0+c}{2}\right)\\ \overline{DB}\mathrm{منتصف} \mathrm{ونقطة}\\ \left(\frac{a+b}{2},\frac{c}{2}\right)=\left(\frac{a+b}{2},\frac{0+c}{2}\right)\end{array}$

إذن $\overline{DB }و \overline{AC}$ ينصف كل منهما الآخر.

تأكد

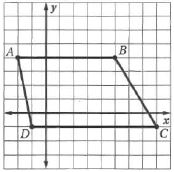
حدد ما إذا كان كل شكل رباعي فيما يأتي متوازي أضلاع أم لا. ثم برر اجابتك.

1)

الحل: نعم لأن كل زاويتين متقابلتين متطابقتين.

2)

الحل:

لا؛ لأنه لا يحقق أي شرط من شروط متوازي الأضلاع.

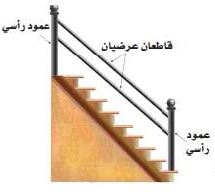
3) نجارة: صنع نجار درابزيناً لدرج يتكون من عمودين رأسيين الأول مثبت فوق الدرجة الأولى والثاني مثبت فوق الدرجة الأخيرة ويصل بينهما قاطعان خشبيان كما في الشكل المجاور كيف يمكن للنجار التحقق من أن القاطعين الخشبيين العرضيين متوازيان وذلك بأقل عدد من مرات القياس إذا علمت بأن الدرجتين الأولى والأخيرة مستويات مع الأرض.

الحل:

إذا كان القاطعان الخشبيان متطابقان فإن الشكل متوازي أضلاع وبالتالي يكون القاطعان الخشبيين متوازيان.

جبر: أوجد x,y في كل مما يأتي بحيث يكون الشكل الرباعي متوازي أضلاع.

4)

الحل:

$\begin{array}{l}8x-8=6x+14\\ \\ 8x-6x=14+8\\ \\ 2x=22\\ \\ x=11\\ \\ 7y+2=6y+16\\ \\ 7y-6y=16-2\\ \\ y=14\end{array}$

5)

الحل:

$\begin{array}{l}x+7=2x+3\\ \\ 2x-x=7-3\\ \\ x=4\\ \\ 3y-5=y+11\\ \\ 3y-y=11+5\\ \\ 2y=16\\ \\ y=8\end{array}$

هندسة إحداثية: مثل في المستوي الإحداثي الشكل الرباعي المعطاة إحداثيات رؤوسه فيما يأتي.

وحدد ما إذا كان متوازي أضلاع أم لا برر اجابتك باستعمال الطريقة المحددة في السؤال.

6) $A(-2,4),B(5,4),C(8,-1),D(-1,-1)$ صيغة الميل.

الحل:

$\begin{array}{r}\frac{-7}{0}=\frac{-2-5}{4-4}:\overline{\mathrm{AB}} \mathrm{ميل} \\ \\ \frac{3}{5}=\frac{5-8}{4+1}:\overline{BC} \mathrm{ميل}\\ \\ \frac{9}{5}=\frac{8+1}{0}:\overline{\mathrm{CD}} \mathrm{ميل}\\ \\ \frac{-1}{5}=\frac{-2+1}{4+1}:\overline{\mathrm{AD} }\mathrm{ميل}\\ \end{array}$

بما أن ميل $\ne \overline{BC}$ميل $\overline{AD}$ فإن ABCD ليس متوازي أضلاع.

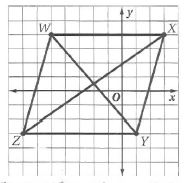
7) $A(-5و4),B(3,4),C(3و-3),D(-7و-3)$ صيغة نقطة المنتصف.

الحل:

نعم؛ نقطة منتصف كل من $\left(-2,\frac{1}{2}\right) \mathrm{هي} \mathrm{XZ}و\overline{\mathrm{WY}}$

وبما أن القطرين ينصف كل منهما الآخر فإن الشكل WXYZ متوازي أضلاع.

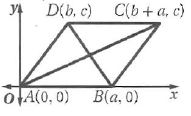
8) اكتب برهاناً إحداثياً للعبارة الآتية: إذا كان الشكل الرباعي متوازي أضلاع، فإن قطريه ينصف كل منهما الآخر.

الحل:

المعطيات: ABCD متوازي أضلاع.

المطلوب: $\overline{AC}$ و $\overline{DB}$ ينصف كل منهما الآخر.

البرهان:

نقطة منتصف $\overline{AC}$

$\begin{array}{r}\left(\frac{a+b}{2},\frac{c}{2}\right)=\left(\frac{0+(a+b)}{2},\frac{0+c}{2}\right)\\ \overline{DB}\mathrm{منتصف} \mathrm{ونقطة}\\ \left(\frac{a+b}{2},\frac{c}{2}\right)=\left(\frac{a+b}{2},\frac{0+c}{2}\right)\end{array}$

إذن $\overline{DB }و \overline{AC}$ ينصف كل منهما الآخر.