إذا كان 120 = TS فأوجد PR.

$\begin{array}{r} \mathrm{معطى} \mathrm{TS}=120\\ \\ \mathrm{الاخر} \mathrm{منهما} \mathrm{كل} \mathrm{ينصف} \mathrm{المستطيل} \mathrm{قطرا} \mathrm{QS}=120\times 2=240\\ \\ \mathrm{متطابقان} \mathrm{القطران} \mathrm{المستطيل} \mathrm{خصائص} \mathrm{من} \mathrm{QS}=\mathrm{PR}=240\end{array}$

تحقق من فهمك

استعن بالشكل في المثال 1.

1A) إذا كان 120 = TS فأوجد PR.

الحل:

$\begin{array}{r} \mathrm{معطى} \mathrm{TS}=120\\ \\ \mathrm{الاخر} \mathrm{منهما} \mathrm{كل} \mathrm{ينصف} \mathrm{المستطيل} \mathrm{قطرا} \mathrm{QS}=120\times 2=240\\ \\ \mathrm{متطابقان} \mathrm{القطران} \mathrm{المستطيل} \mathrm{خصائص} \mathrm{من} \mathrm{QS}=\mathrm{PR}=240\end{array}$

1B) اذا كان $m\angle PRS = 64°$ فأوجد $m\angle SQR$

الحل:

الزوايا الأربع قوائم للمستطيل.

إذن $\angle SRQ = 90°$

$\mathrm{\angle }\mathrm{QRT}=\mathrm{\angle }\mathrm{SQR}={90}^{\circ }-{64}^{\circ }={26}^{\circ }$

2) استعن بالشكل في المثال 2. إذا كان $JP=3y-5 , MK=5y+1$ فأوجد قيمة y.

الحل:

قطرا المستطيل متطابقان وينصف كل منهما الآخر.

$\begin{array}{l}\mathrm{MK}=\mathrm{LJ}\\ \\ \mathrm{MK}=(\mathrm{JP}+\mathrm{PL})\\ \\ \because \mathrm{JP}=\mathrm{PL}\\ \\ \therefore \mathrm{MK}=2\left(\mathrm{JP}\right)\\ \\ 5\mathrm{y}+1=2(3\mathrm{y}-5)\\ \\ 5\mathrm{y}+1=6\mathrm{y}-10\\ \\ 6\mathrm{y}-5\mathrm{y}=1+10\\ \\ \mathrm{y}=11\end{array}$

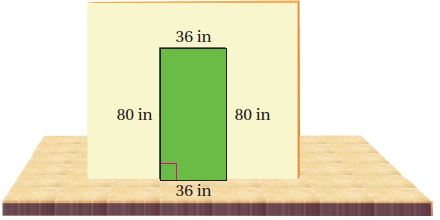
3) تصميم: بالرجوع الى فقرة "لماذا؟" بداية الدرس قاس أحمد أبعاد المنطقة التي قام بطلائها كما في الشكل أدناه وباستعمال زاوية النجارين تحقق من أن الزاوية عند الركن الأيسر السفلي قائمة فهل يمكنه استنتاج أن المنطقة مستطيلة الشكل؟ وضح إجابتك.

الحل:

نعم؛ بما أن الأضلاع المتقابلة متطابقة فإن المنطقة التي قام بطلائها تشكل متوازي أضلاع واذا كانت إحدى زوايا متوازي أضلاع قائمة فإن جميع الزوايا قائمة وبما أن الزاوية السفلى إلى يسار القائمة فإن جميع الزوايا قائمة لذلك وحسب التعريف يكون المدخل مستطيلاً.

4) إذا كانت إحداثيات رؤوس الشكل الرباعي jklm هي $J(-10,2), K(-8,-6), L(5,-3), M(2,5)$

فهل jklm مستطيل؟ استعمل صيغة الميل.

الحل:

$\begin{array}{r}\frac{-1}{4}=\frac{-2}{8}=\frac{-10+8}{2+6}:\overline{\mathrm{JK}} \mathrm{ميل}\\ \\ \frac{3}{-8}=\frac{5-2}{-3-5}:\overline{\mathrm{ML}} \mathrm{ميل}\end{array}$

بما أن ميل $\overline{JK}$ لا يساوي ميل $\overline{ML}$, أي أنهما غير متوازيان إذن JKLM ليس مستطيلاً.