اكتب معادلات أربع مستقيمات بحيث تكون نقاط تقاطعها رؤوس مستطيل تحقق من إجابتك باستعمال الهندسة الإحداثية.

x = 0, x = 6, y = 0, y = 4

طول يساوي أو وحدات وطول يساوي أو وحدات ميل يساوي صفراً وميل يساوي صفراً.

وبما أن ضلعين للشكل الرباعي متوازيان ومتطابقان، فإنه وبحسب النظرية 1.12 يكون متوازي أضلاع.

لأن أفقي ورأسي فإن المستقيمين متعامدان وقياس الزاوية التي يشكلها وحسب النظرية 1.6 إذا كان لمتوازي أضلاع زاوية قائمة فإن زواياه الأربع قوائم لذلك وحسب التعريف يكون متوازي الاضلاع مستطيلاً.

مسائل مهارات التفكير العليا

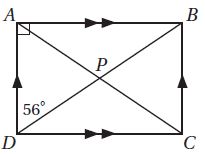
39) تحدٍ: في المستطيل ABCD إذا كان $m\mathrm{\angle }FAB=(4x+6{)}^{\circ }, m\mathrm{\angle }DEC=(10-11y{)}^{\circ },m\mathrm{\angle }EBC={60}^{\circ }$ فأوجد قيمة كل من x,y.

الحل:

$\begin{array}{l}\mathrm{\angle }\mathrm{ABE}+\mathrm{\angle }\mathrm{EBC}=90\\ \\ \mathrm{\angle }\mathrm{ABE}+60=90\\ \\ \mathrm{\angle }\mathrm{ABE}=30\\ \\ 4\mathrm{x}+6=30\\ \\ 4\mathrm{x}=30-6\\ \\ 4\mathrm{x}=24\\ \\ \mathrm{x}=6\\ \\ \mathrm{\angle }\mathrm{AEB}=180-2\left(30\right)\\ \\ \mathrm{\angle }\mathrm{AEB}=\mathrm{\angle }\mathrm{EDC}=120\\ \\ 10-11\mathrm{y}=120\\ \\ -11\mathrm{y}=120-10\\ \\ \mathrm{y}=\frac{-110}{11}=-10\end{array}$

40) اكتشف الخطأ: قالت بسمة: إن أي مثلثين حادي الزوايا ومتطابقين يمكن ترتيبهما ليشكلا مستطيلاً وقالت شيماء: إن المثلثين القائمي الزاوية المتطابقين هما فقط اللذان يمكن ترتيبهما ليشكلا مستطيلاً هل أي منهما على صواب؟ وضح تبريرك.

الحل:

شيماء؛ عندما يرتب مثلثان متطابقان ليشكلا شكلاً رباعياً فإن زاويتين من زوايا الشكل الرباعي ناتجتان من رأس منفرد لمثلث ولكي يكون الشكل الرباعي مستطيلاً يجب أن تكون إحدى الزوايا في المثلثين المتطابقين قائمة.

41) مسألة مفتوحة: اكتب معادلات أربع مستقيمات بحيث تكون نقاط تقاطعها رؤوس مستطيل تحقق من إجابتك باستعمال الهندسة الإحداثية.

الحل:

x = 0, x = 6, y = 0, y = 4

طول يساوي أو وحدات وطول يساوي أو وحدات ميل يساوي صفراً وميل يساوي صفراً.

وبما أن ضلعين للشكل الرباعي متوازيان ومتطابقان، فإنه وبحسب النظرية 1.12 يكون متوازي أضلاع.

لأن أفقي ورأسي فإن المستقيمين متعامدان وقياس الزاوية التي يشكلها وحسب النظرية 1.6 إذا كان لمتوازي أضلاع زاوية قائمة فإن زواياه الأربع قوائم لذلك وحسب التعريف يكون متوازي الاضلاع مستطيلاً.

42) اكتب: وضح لم تعد جميع المستطيلات متوازيات أضلاع بينما لا تعد جميع متوازيات الأضلاع مستطيلات.

الحل:

كل المستطيلات تكون متوازيات أضلاع لأنه بناء على تعريف المستطيل يكون كل ضلعين متقابلين فيه متوازيين ومتوازي الأضلاع الذي تكون زواياه قوائم يكون مستطيلاً لذا تكون بعض متوازيات الأضلاع مستطيلات وأما بعضها الآخر الذي زواياه ليست قوائم فلا تكون مستطيلات.

43) في الشكل الرباعي FGHJ إذا كان $FM=3x+y,GH=11,GM=13 , FJ=-3x+5y$ فما قيمة كل من x, y اللتين تجعلان FGHJ مستطيلاً؟

• x=3,y=4
• x=4,y=3
• x=7,y=8
• x=8,y=7

الحل:

A

$\begin{array}{l}\mathrm{FJ}=\mathrm{GH}\\ \\ -3\mathrm{x}+5\mathrm{y}=11\to 1\\ \\ \mathrm{GM}=13\\ \\ 3\mathrm{x}+\mathrm{y}=13\to 2\\ \\ 6\mathrm{y}=24\\ \\ \mathrm{y}=4\\ \\ 3\mathrm{x}+\mathrm{y}=13\\ \\ 3\mathrm{x}+4=13\\ \\ 3\mathrm{x}=13-4\\ \\ 3\mathrm{x}=9\\ \\ \mathrm{x}=3\end{array}$

44) إجابة قصيرة: ما قياس $\angle APB$؟

الحل:

بالتبادل داخلياً زوايا المستطيل قائمة (قطرا المستطيل متطابقان وينصف كل منهما الآخر).

$\begin{array}{l}\mathrm{\angle }\mathrm{DBC}={56}^{\circ }\\ \\ \mathrm{\angle }\mathrm{ABD}={90}^{\circ }-{56}^{\circ }=34\\ \\ \mathrm{PB}=\mathrm{AP}\\ \\ \therefore \mathrm{\angle }\mathrm{BAP}=34\\ \\ \mathrm{\angle }\mathrm{APB}={180}^{\circ }-(34+34)\\ \\ \mathrm{\angle }\mathrm{APB}={180}^{\circ }-{68}^{\circ }\\ \\ \mathrm{\angle }\mathrm{APB}={112}^{\circ }\end{array}$