يتكون نمط الفسيفساء المبين جانباً من قطع ثمانية منتظمة وأخرى رباعية صنف الأشكال في النمط ووضح تبريرك.

مربعات: إجابة ممكنة: بما أن الثمانيات منتظمة فإن الأضلاع متطابقة وتشترك الأشكال الرباعية مع الثمانيات في الأضلاع لذا فإن الأشكال الرباعية معينات أو مربعات.

وزوايا رؤوس الأشكال الرباعية تتكون من الزوايا الخارجية لأضلاع الثمانيات المجاور للرؤوس.

ومجموع قياسات الزوايا الخارجية لأي مضلع يساوي 360º دائماً ولأن الثماني المنتظم له 8 زوايا خارجية متطابقة فإن قياس كل منها يساوي 45º وكما هو مبين في الشكل فإن قياس كل زاوية للأشكال الرباعية في النمط يساوي 45º + 45º أو 90º لذلك فالشكل الرباعي يكون مربعاً.

تدرب وحل المسائل

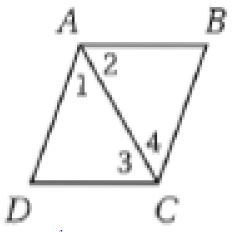
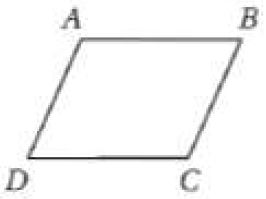
جبر: استعن بالمعين ABCD المعين جانباً.

7) إذا كان AB = 14 فأوجد BC.

الحل:

خصائص المعين الأضلاع المتتالية متطابقة.

BC = AB =14

8) إذا كان $m\angle BCD = 118°$ فأوجد $m\angle BAC$.

الحل:

الزاويتان المتقابلتان متطابقتان وقطرا المعين ينصف الزاوية.

$\begin{array}{r}\mathrm{\angle }\mathrm{BCD}=\mathrm{\angle }\mathrm{BAD}=118\\ \\ \mathrm{\angle }\mathrm{BCD}=\frac{118}{2}={59}^{\circ }\end{array}$

9) إذا كان AP = 3x – 1 وPC = x + 9 فأوجد AC.

الحل:

$\begin{array}{l}\mathrm{AP}=\mathrm{PC}\\ \\ 3\mathrm{x}-1=\mathrm{x}+9\\ \\ 2\mathrm{x}=9+1\\ \\ 2\mathrm{x}=10\\ \\ \mathrm{x}=5\\ \\ \mathrm{AC}=\mathrm{AP}+\mathrm{PC}\\ \\ \mathrm{AC}=3\mathrm{x}-1+\mathrm{x}+9\\ \\ \mathrm{AC}=15-1+5+9\\ \\ \mathrm{AC}=28\end{array}$

10) إذا كان $m\mathrm{\angle }BCD=(2x+3{)}^{\circ },m\mathrm{\angle }ABC=(2x-7{)}^{\circ }$ فأوجد $m\angle DAB$.

الحل:

الزاويتان المتحالفتان متكاملتان.

$\begin{array}{l}\mathrm{m}\mathrm{\angle }\mathrm{ABC}+\mathrm{m}\mathrm{\angle }\mathrm{BCD}={180}^{\circ }\\ \\ 2\mathrm{x}-7+2\mathrm{x}+3={180}^{\circ }\\ \\ 4\mathrm{x}-4={180}^{\circ }\\ \\ 4\mathrm{x}=184\\ \\ \mathrm{x}=46\\ \\ \mathrm{m}\mathrm{\angle }\mathrm{BCD}=2\mathrm{x}+3\\ \\ \mathrm{m}\mathrm{\angle }\mathrm{BCD}=95\\ \\ \mathrm{m}\mathrm{\angle }\mathrm{DAB}=\mathrm{m}\mathrm{\angle }\mathrm{BCD}={95}^{\circ }\mathrm{متطابقة} \mathrm{المتناظرة} \mathrm{الزوايا} \end{array}$

11) إذا كان $m\mathrm{\angle }DPC=(3x-15{)}^{\circ }$ فأوجد قيمة x.

الحل:

$\begin{array}{l}\mathrm{m}\mathrm{\angle }\mathrm{DPC}=3\mathrm{x}-15=90\\ \\ 3\mathrm{x}=15+90\\ \\ 3\mathrm{x}=105\\ \\ \mathrm{x}=35\end{array}$

برهان: اكتب برهاناً ذا عمودين في كل مما يأتي:

12) المعطيات: QRST متوازي أضلاع.

$\overline{TR}\cong \overline{QS},m\mathrm{\angle }QPR={90}^{\circ }$

المطلوب: QRST مربع.

الحل:

• المعطيات: QRST متوازي أضلاع $\mathrm{m}\mathrm{\angle }\mathrm{QPR}={90}^{\circ }؛\overline{\mathrm{TR}}\cong \overline{\mathrm{QS}}$
• المطلوب: QRST مربع.
• العبارات: (المبررات):

1) QRST متوازي أضلاع $\mathrm{m}\mathrm{\angle }QPR={90}^{\circ }؛\overline{TR}\cong \overline{QS}$ (معطيات).

2)QRST مستطيل (إذا كان قطرا متوازي أضلاع متطابقين فإنه مستطيل).

3) $\angle QPR$قائمة (تعريف الزاوية القائمة).

4) $\overline{QS}\perp \overline{TR}$ (تعريف التعامد).

5) QRST معين (إذا كان قطرا متوازي أضلاع متعامدين فإنه معين).

6) QRST مربع (النظرية 1.2؛ إذا كان الشكل الرباعي مستطيلاً) ومعيناً فإنه مربع.

13) المعطيات: JKQP مربع $\overline{ML}$ تنصف كلاً من $\overline{KQ}و\overline{JP}$.

المطلوب: JKLM متوازي أضلاع.

الحل:

البرهان: العبارات (المبررات).

1) JKQP مربع. $\overline{ML}$ تنصف كلاً من $\overline{JP}$ و $\overline{KQ}$ (معطيات).

2) JKQP متوازي أضلاع (جميع المربعات متوازيات أضلاع).

3) $\overline{JK}\parallel \overline{ML}$ ( تعريف متوازي الأضلاع).

4) $\overline{JP}\cong \overline{KQ}$ (الأضلاع المتقابلة لمتوازي الأضلاع متطابقة).

5) $JP = KQ$ (تعريف تطابق القطع المستقيمة).

6) JM =MP , KL = LQ (تعريف المنصف)

7) JP + JM = MP ,KQ = KL + LQ (مسلمة جمع القطع المستقيمة).

8) JP = 2JM , KQ = 2KL (بالتعويض).

9) 2JM = 2KL (بالتعويض).

10) JM = KL (خاصية).

11) KL = JM (تعريف تطابق القطع المستقيمة).

12) JKLM متوازي أضلاع (إذا وجد ضلعان متقابلان في شكل رباعي متطابقين ومتوازيين فإنه متوازي أضلاع).

14) طريق: يتقاطع طريقان كما في الشكل إذا كانت ممرات المشاة لها الطول نفسه فصنف الشكل الرباعي المكون من هذه الممرات ووضح تبريرك.

الحل:

معين قياس الزاوية المتكونة بين الشارعين 60º والزاويتان المتقابلتان بالرأس متطابقتان لذلك فقياس إحدى زوايا الشكل الرباعي 29º وبما أن لممري المشاة الطول نفسه فإن أضلاع الشكل الرباعي متطابقة لذلك فإنها تشكل معيناً.

15) زراعة: حدد مزارع حقلاً بأوتاد وحبال كما في الشكل المجاور.

إذا كانت أضلاع الشكل الرباعي المتشكل متساوية الطول وقطراه متعامدين فهل هذه المعلومات كافية كي تتحقق من أن الحقل مربع؟ وضح تبريرك.

الحل:

لا؛ إجابة ممكنة: بما أن الأضلاع الأربعة للشكل الرباعي متطابقة وقطريه متعامدان فإن الشكل مربع أو معين وللتحقق من أن الحقل مربع يحتاج المزارع إلى إثبات أن القطرين متطابقين.

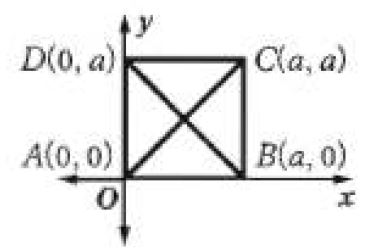
هندسة إحداثية: حدد ما إذا كان $▱JKLM$ المعطاة إحداثيات رؤوسه في كل مما يأتي معيناً أو مستطيلاً أو مربعاً اكتب جميع التسميات التي تنطبق عليه ووضح إجابتك.

16) J(-4,-1), K(1-1), L(4,3), M(-1,3)

الحل:

اولاً: استعمل صيغة المسافة بين نقطتين للمقارنة بين طولي القطرين.

$\begin{array}{r}\mathrm{JL}=\sqrt{(-4-4{)}^2+(-1-3{)}^2}=\sqrt{80}\\ \\ \mathrm{KM}=\sqrt{(1+1{)}^2+(-1-3{)}^2}=\sqrt{20}\end{array}$

بما أن القطران JL ,KM ليس متساويان إذن هما غير متطابقان إذن الشكل ليس مستطيل وليس مربع.

ثانياً: استعمل صيغة الميل لتحديد ما إذا كان القطران متعامدان.

$\begin{array}{c}2=\frac{-8}{-4}=\frac{-4-4}{-1-3}=\overline{\mathrm{JL}} \mathrm{ميل}\\ \\ \frac{-1}{2}=\frac{-2}{4}=\frac{1+1}{-1-3}=\overline{\mathrm{KM}} \mathrm{ميل}\end{array}$

بما أن حاصل ضرب الميلين =1- فإن القطرين متعامدان لذا فأن JKLM معين.

إذن الشكل معين لأن قطريه متعامدان وغير متطابقين.

17) J(-3,-2), K(2,-2), L(5,2), M(0,2)

الحل:

اولاً: استعمل صيغة المسافة بين نقطتين للمقارنة بين طولي القطرين.

$\begin{array}{r}\mathrm{JL}=\sqrt{(-3-5{)}^2+(-2-2{)}^2}=\sqrt{80}\\ \\ \mathrm{KM}=\sqrt{(2-0{)}^2+(-2-2{)}^2}=\sqrt{20}\end{array}$

بما أن القطران JL, KM ليس متساويان إذن هما غير متطابقان إذن الشكل JKLM ليس مستطيل وليس مربع.

ثانياً: استعمل صيغة الميل لتحديد ماذا كان القطران متعامدان.

$\begin{array}{r}2=\frac{-8}{-4}=\frac{-3-5}{-2-2}=\overline{\mathrm{JL}} \mathrm{ميل}\\ \\ \frac{-1}{2}=\frac{2}{-4}=\frac{2-0}{-2-2}=\overline{\mathrm{KM}} \mathrm{ميل}\end{array}$

بما أن حاصل ضرب الميلين =1- فإن القطرين متعامدان لذا فأن JKLM معين.

إذن الشكل معين لأن قطريه متعامدان وغير متطابقين.

18) J(-2,-1), K(-4,3), L(1,5), M(3,1)

الحل:

أولاً: استعمل صيغة المسافة بين نقطتين للمقارنة بين طولي القطرين.

$\begin{array}{r}\mathrm{JL}=\sqrt{(-2-1{)}^2+(-1-5{)}^2}=\sqrt{45}\\ \\ \mathrm{KM}=\sqrt{(-4-3{)}^2+(3-1{)}^2}=\sqrt{53}\end{array}$

بما أن القطران JL, KM ليس متساويان إذن هما غير متطابقان إذن الشكل JKLM ليس مستطيل وليس مربع.

ثانياً: استعمل صيغة الميل لتحديد ماذا كان القطران متعامدان.

$\begin{array}{r}\frac{1}{2}=\frac{3}{6}=\frac{-2-1}{-1-5}=\overline{\mathrm{JL}} \mathrm{ميل}\\ \\ \frac{-7}{2}=\frac{-4-3}{3-1}=\overline{\mathrm{KM}} \mathrm{ميل}\end{array}$

بما أن حاصل ضرب الميلين $\ne$1- فإن القطرين غير متعامدين لذا فإن JKLM ليس معين.

إذن الشكل لا شيء لأن قطريه غير متعامدان وغير متطابقين.

19) J(-1,1), K(4,1), L(4,6), M(-1,6)

الحل:

أولاً: استعمل صيغة المسافة بين نقطتين للمقارنة بين طولي القطرين.

$\begin{array}{r}\mathrm{JL}=\sqrt{(-1-4{)}^2+(1-6{)}^2}=\sqrt{50}\\ \\ \mathrm{KM}=\sqrt{(4+1{)}^2+(1-6{)}^2}=\sqrt{50}\end{array}$

بما أن القطران JL, KM متساويان إذن هما غير متطابقان إذن الشكل JKLM مستطيل.

ثانياً: استعمل صيغة الميل لتحديد ماذا كان القطران متعامدان.

$\begin{array}{r}1=\frac{-5}{-5}=\frac{-1-4}{1-6}=\overline{\mathrm{JL}} \mathrm{ميل}\\ \\ -1=\frac{5}{-5}=\frac{4+1}{1-6}=\overline{\mathrm{KM}} \mathrm{ميل}\end{array}$

بما أن حاصل ضرب الميلين =1- فإن القطرين متعامدين لذا فإن JKLM معين.

إذن الشكل مستطيل ومربع ومعين لأن جميع أضلاعه متطابقة وجميع زواياه قوائم.

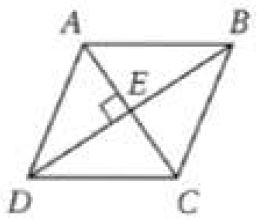
في المعين ABCD إذا كان $PB = 12 , AB = 15 , m\angle ABD = 24°$ فأوجد كلا مما يأتي:

20) AP

الحل:

بما أن الشكل معين إذن القطران متعامدان إذن $△APB$قائم الزاوية وباستخدام فيثاغورث ينتج أن:

$\begin{array}{l}(\mathrm{AB}{)}^2=(\mathrm{AP}{)}^2+(\mathrm{PB}{)}^2\\ \\ (15{)}^2=(\mathrm{AP}{)}^2+(12{)}^2\\ \\ 225=(\mathrm{AP}{)}^2+144\\ \\ (\mathrm{AP}{)}^2=81\\ \\ \mathrm{AP}=9\\ \end{array}$

21) CP

الحل:

AP = CP = 9

22) $m\angle BDA$.

الحل:

من خصائص المعين أن الأضلاع المتجاورة متطابقة وبالتالي يكون $△ADB$متطابق الضلعين وبالتالي يكون زوايا القاعدة متساوية.

$\begin{array}{l}\because \mathrm{AB}=\mathrm{AD}\\ \\ \mathrm{\angle }\mathrm{ABD}=\mathrm{\angle }\mathrm{BDA}={24}^{\circ }\end{array}$

23) $m\angle ACB$

الحل:

$\begin{array}{l}\mathrm{\angle }\mathrm{DCB}=180-(\mathrm{\angle }\mathrm{DBC}+\mathrm{\angle }\mathrm{BDC})\\ \\ \mathrm{\angle }\mathrm{DCB}=180-(24+24)\\ \\ \mathrm{\angle }\mathrm{DCB}=132\\ \\ \mathrm{\angle }\mathrm{ACB}=\frac{132}{2}={66}^{\circ }\end{array}$

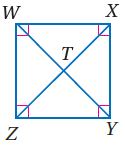
في المربع WXYZ إذا كان WT = 3 فأوجد كلا مما يأتي:

24) ZX

الحل:

من خصائص المربع القطران متطابقان وينصف كل منهما الآخر.

$\begin{array}{l}\mathrm{WT}=\mathrm{TY}=3\\ \\ \mathrm{WY}=2\times 3=6\\ \\ \mathrm{WY}=\mathrm{ZX}=6\end{array}$

25) XY

الحل:

$\begin{array}{l}(\mathrm{XY}{)}^2=(\mathrm{XT}{)}^2+(\mathrm{TY}{)}^2\\ \\ (\mathrm{XY}{)}^2=(3{)}^2+(3{)}^2\\ \\ (\mathrm{XY}{)}^2=18\\ \\ \mathrm{XY}=3\sqrt{2}\end{array}$

26) $m\angle WTZ$.

الحل:

من خصائص المربع أن قطراه متعامدان.

$\angle WTZ = 90°$

27) $m\angle WXY$

الحل:

$\angle WYX = \frac{90}{2} = 45°$

برهان: اكتب برهاناً حراً لكل مما يأتي:

28) النظرية 1.16

الحل:

المعطيات: ABCD معين.

المطلوب: إثبات أن كل قطر ينصف زاويتين متقابلتين.

البرهان: نعلم أن ABCD معين وحسب تعريف المعين يكون ABCD متوازي أضلاع وبما أن الزوايا المتقابلة في متوازي الأضلاع متطابقة فإن $\cdot \mathrm{\angle }\mathrm{BAD}\cong \mathrm{\angle }\mathrm{BCD} \text{و }\mathrm{\angle }\mathrm{ABC}\cong \mathrm{\angle }\mathrm{ADC}$ولأن جميع أضلاع المعين متطابقة فإن $\overline{AB}\cong \overline{BC}\cong \overline{CD}\cong \overline{DA}$ وحسب SAS يكون $△ABC \cong △ADC$ اذن $\angle 7 \cong \angle 8 و \angle 5 \cong \angle 6$

لأن العناصر المتناظرة في المثلثين المتطابقين متطابقة وكذلك$△BAD \cong △BCD$ وحسب SAS ولذا $\angle 1 \cong \angle 2 و \angle 3 \cong \angle 4$ لأن العناصر المتناظرة في المثلثين المتطابقين متطابقة ومن تعريف منصف الزاوية فإن كل قطر ينصف زاويتين متقابلتين.

29) النظرية 1.17

الحل:

• المعطيات: ABCD متوازي أضلاع؛ $\overline{AC}\perp \overline{BD}$
• المطلوب: ABCD معين.

البرهان: نعلم أن ABCD متوازي أضلاع وبما أن قطري متوازي الأضلاع ينصف كل منهما الآخر فإن $\overline{AE}\cong \overline{EC}$ وكذلك $\overline{BE}\cong \overline{BE}$ لأن تطابق القطع المستقيمة يحقق خاصية الانعكاس.

ونعلم أيضاً أن $\overline{AC}\perp \overline{BD}$ إذن $\angle BEC و \angle AEB$ قائمتان حسب تعريف المستقيمين المتعامدين.

إذن $\angle AEB \cong \angle BEC$ لأن جميع الزوايا القائمة متطابقة.

لذلك $△AEB \cong △BEC$ بحسب SAS.

إذن $\overline{AB}\cong \overline{CB}$ لأن العناصر المتناظرة في المثلثين المتطابقين متطابقة.

وبما أن الأضلاع المتقابلة في متوازي الأضلاع متطابقة.

فإن $\overline{\mathrm{AB}}\cong \overline{\mathrm{CD}}\cong \overline{\mathrm{CB}}\cong \overline{\mathrm{AD}}ن\text{إذ }\overline{\mathrm{CB}}\cong \overline{\mathrm{AD}}و\overline{\mathrm{AB}}\cong \overline{\mathrm{CD}}$ تطابق القطع المستقيمة يحقق خاصية التعدي.

وبما أن جميع أضلاع الشكل ABCD متطابقة فإنه معين حسب التعريف.

30) النظرية 1.18

الحل:

• المعطيات: ABCD متوازي أضلاع القطر $\overline{AC}$ ينصف كلاً من $\angle BCD , \angle DAB$.
• المطلوب: ABCD معين.

البرهان: نعلم أن ABCD متوازي أضلاع.

وبما أن الأضلاع المتقابلة في متوازي الأضلاع متوازية فإن $\overline{AB}\parallel \overline{DC}$ وحسب التعريف $\angle 3 و \angle 2$ متبادلتان داخلياً بالنسبة للضلعين المتوازيين $\overline{DC} و \overline{AB}$

وبما أن الزاويتين المتبادلتين داخلياً متطابقتان فإن $\angle 2 \cong \angle 3$

ولأن تطابق الزوايا يحقق خاصية التماثل فإن $\angle 2 \cong \angle 3$ ونعلم أن $\overline{AC}$ تنصف كل من $\angle BCD و \angle DAB$ إذن $\angle 3 \cong \angle 4 و \angle 1 \cong \angle 2$ حسب التعريف.

ومن خاصية التعدي $\angle 2 \cong \angle 4 و \angle 1 \cong \angle 3$

ولأن الأضلاع المقابلة للزوايا المتطابقة في مثلث تكون متطابقة فإن $\overline{AB}\cong \overline{AD} و \overline{BC} \cong \overline{DC}$

إذن ولأن ضلعين متجاورين في متوازي الأضلاع متطابقان فإن ABCD معين.

31) النظرية 1.18

الحل:

• المعطيات: ABCD متوازي أضلاع $\overline{AB}\cong \overline{BC}$.
• المطلوب: ABCD معين.

البرهان: بما أن الأضلاع المتقابلة في متوازي الأضلاع متطابقة فإن $\overline{AB}\cong \overline{CD}و\overline{AD}\cong \overline{BC}$ ونعلم أيضاً أن $\overline{AB}\cong \overline{BC}$.

وحسب خاصية التعدي تكون $\overline{BC}\cong \overline{CD}$ إذن $\overline{\mathrm{BC}}\cong \overline{\mathrm{CD}}\cong \overline{\mathrm{AB}}\cong \overline{\mathrm{AD}}$ لذلك ABCD معين حسب التعريف.

32) النظرية 1.20

الحل:

المعطيات: ABCD مستطيل ومعين.

المطلوب: ABCD مربع.

البرهان: نعلم أن ABCD مستطيل ومعين.

إذن ABCD متوازي أضلاع أيضاً لأن جميع المستطيلات والمعينات متوازي أضلاع وحسب تعريف المستطيل فإن $\angle A , \angle B , \angle C , \angle D$ جميعها قوائم وحسب تعريف المعين جميع الأضلاع متطابقة لذلك ABCD مربع لأنه متوازي أضلاع أضلاعه الأربعة متطابقة وزواياه الأربع قوائم

برهان: اكتب برهاناً إحداثياً للعبارة في كل من السؤالين الآتيين:

33) قطرا المربع متعامدان.

الحل:

المعطيات: ABCD مربع.

المطلوب: $\overline{AC}\perp \overline{DB}$.

البرهان:

$\begin{array}{r}-1=\frac{0-a}{a-0}=m:\overline{DB} \mathrm{ميل}\\ \\ 1=\frac{0-a}{0-a}=m:\overline{AC} \mathrm{ميل}\end{array}$

بما أ ميل $\overline{AC}$ يساوي سالب مقلوب ميل $\overline{DB}$ فإنهما متعامدان.

34) تشكل القطع المستقيمة الواصلة بين منتصفات أضلاع مستطيلاً معيناً.

الحل:

• المعطيات: ABCD مستطيل Q,R,S,T منتصفات أضلاع المستطيل.
• المطلوب: QRST معين
• البرهان: إحداثيات نقطة المنتصف Q هي:

$\left(\frac{0+0}{2},\frac{b+0}{2}\right)=\left(0,\frac{b}{2}\right)$

إحداثيات نقطة المنتصف R هي:

$\left(\frac{a+0}{2},\frac{b+b}{2}\right)=\left(\frac{a}{2},\frac{2b}{2}\right)=\left(\frac{a}{2},b\right)$

إحداثيات نقطة المنتصف T هي:

$\left(\frac{\mathbf{a}+\mathbf{0}}{2},\frac{\mathbf{0}+\mathbf{0}}{2}\right)=\left(\frac{\mathbf{a}}{2},0\right)$

$\begin{array}{r}\mathrm{QR}=\sqrt{{\left(\frac{\mathrm{a}}{2}-0\right)}^2+{\left(\mathrm{b}-\frac{\mathrm{b}}{2}\right)}^2}=\sqrt{{\left(\frac{\mathrm{a}}{2}\right)}^2+{\left(\frac{\mathrm{b}}{2}\right)}^2}\\ \\ \mathrm{RS}=\sqrt{{\left(\mathrm{a}-\frac{\mathrm{a}}{2}\right)}^2+{\left(\frac{\mathrm{b}}{2}-\mathrm{b}\right)}^2}=\sqrt{{\left(\frac{\mathrm{a}}{2}\right)}^2+{\left(-\frac{\mathrm{b}}{2}\right)}^2}\\ \\ =\sqrt{{\left(\frac{\mathrm{a}}{2}\right)}^2+{\left(\frac{\mathrm{b}}{2}\right)}^2}\\ \\ \mathrm{ST}=\sqrt{{\left(\mathrm{a}-\frac{\mathrm{a}}{2}\right)}^2+{\left(\frac{\mathrm{b}}{2}-0\right)}^2}=\sqrt{{\left(\frac{\mathrm{a}}{2}\right)}^2+{\left(\frac{\mathrm{b}}{2}\right)}^2}\\ \\ \text{ QT }=\sqrt{{\left(\frac{\mathrm{a}}{2}-0\right)}^2+{\left(0-\frac{b}{2}\right)}^2}=\sqrt{{\left(\frac{\mathrm{a}}{2}\right)}^2+{\left(-\frac{\mathrm{b}}{2}\right)}^2}\\ \\ =\sqrt{{\left(\frac{\mathrm{a}}{2}\right)}^2+{\left(\frac{\mathrm{b}}{2}\right)}^2}\end{array}$

بما أن QR = RS = ST = QT فإن $\overline{ST}\cong \overline{QT}\cong \overline{RS}\cong \overline{RQ}$ إذن QRST معين.

35) تصميم: يتكون نمط الفسيفساء المبين جانباً من قطع ثمانية منتظمة وأخرى رباعية صنف الأشكال في النمط ووضح تبريرك.

الحل:

مربعات: إجابة ممكنة: بما أن الثمانيات منتظمة فإن الأضلاع متطابقة وتشترك الأشكال الرباعية مع الثمانيات في الأضلاع لذا فإن الأشكال الرباعية معينات أو مربعات.

وزوايا رؤوس الأشكال الرباعية تتكون من الزوايا الخارجية لأضلاع الثمانيات المجاور للرؤوس.

ومجموع قياسات الزوايا الخارجية لأي مضلع يساوي 360º دائماً ولأن الثماني المنتظم له 8 زوايا خارجية متطابقة فإن قياس كل منها يساوي 45º وكما هو مبين في الشكل فإن قياس كل زاوية للأشكال الرباعية في النمط يساوي 45º + 45º أو 90º لذلك فالشكل الرباعي يكون مربعاً.

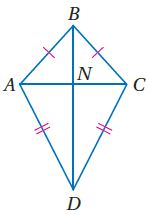
36) تمثيلات متعددة: سوف تستقصي في هذه المسألة إحدى خصائص شكل الطائرة الورقية وهو شكل رباعي يتكون من زوجين متمايزين من الأضلاع المتجاورة والمتطابقة.

a) هندسياً: ارسم قطعة مستقيمة ثم افتح الفرجار وثبته عند أحد طرفيها وارسم قوساً فوقها ومن دون تغيير فتحة الفرجار ثبت رأس الفرجار عند الطرف الآخر للقطعة المستقيمة وارسم قوساً يقطع القوس السابق غير فتحة الفرجار وارسم قوسين أسفل القطعة المستقيمة كما فعلت سابقاً.

استعمل وصل بين طرفَي القطعة والأقواس وسينتج لك شكل طائرة ورقية سمّها ABCD ثم كرِّر ذلك مرتين وسمِّ شكلي الطائرتين الورقيتين PQRS WXYZ ثم ارسم قطري كل منهما ولتكن نقطة تقاطع قطري كل منها N.

الحل:

b) جدولياً: استعمل مسطرة لقياس المسافة من N إلى كل رأس وسجل النتائج في جدول على النحو الآتي:

c) لفظياً: اكتب تخميناً حول قطري شكل الطائرة الورقية.

الحل: القطر الأول في شكل الطائرة الورقية ينصف القطر الآخر.