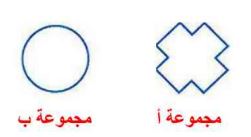
وضع التصميم المستطيلي والروماني في المجموعة (أ) والأحواض الثلاثة الباقية في المجموعة (ب) صف اختلافاً واحداً بين أشكال الأحواض في المجموعتين.

الاختلاف أن أشكال المجموعة أ مكونة من خطوط مستقيمة؛ ولكن أشكال المجموعة ب عبارة عن منحنيات.

حل أسئلة تحقق من فهمك

١- وضع التصميم المستطيلي والروماني في المجموعة (أ) والأحواض الثلاثة الباقية في المجموعة (ب) صف اختلافاً واحداً بين أشكال الأحواض في المجموعتين.

الاختلاف أن أشكال المجموعة أ مكونة من خطوط مستقيمة؛ ولكن أشكال المجموعة ب عبارة عن منحنيات.

٢- ارسم تصميمين لحوضي سباحة بحيث يمكن إضافة أحداهما إلى المجموعة (أ) والآخر إلى المجموعة (ب).

أي الشكلين الآتيين مضلع؟ وهل هو منتظم أم لا؟ وإذا كان مضلعاً فصنفه وإذا لم يكن مضلعاً فاذكر السبب.

أ.

الشكل ليس مضلعاً، لأنه شكل مفتوح.

ب.

الشكل له ٥ أضلاع غير متطابقين و٤ زوايا غير متطابقة، الشكل خماسي غير منتظم.

أوجد قياس الزاوية في كل مضلع مما يأتي:

جـ. مضلع ثماني منتظم.

نقسم الشكل الثماني إلى أربع مثلثات وبما أن مجموع قياسات زوايا المثلث = ١٨٠°

مجموع قياسات زوايا الثماني = ١٨٠ × ٤ = ٧٢٠°

٨ ن = ٧٢٠°

ن = ٩٠°

قياس كل زاوية من المضلع الثماني المنظم = ٩٠°

د. مثلث متطابق الأضلاع.

بما أن المثلث متطابق الأضلاع؛ إذاً متطابق الزوايا.

٣ ن = ١٨٠°

ن = ٦٠°

قياس كل زاوية في المثلث المتطابق الأضلاع = ٦٠°

هـ. تصميم: هل يستطيع علي استعمال على شكل مثلثات متطابقة الأضلاع لتبليط أرضية غرفته؟ وضح إجابتك.

يجب أن يكون مجموع زوايا الرؤوس الملتقية ٣٦٠°

٦٠ ن = ٣٦٠° بقسمة الطرفين على ٦٠

ن = ٦

بما أن ٣٦٠ تقبل القسمة على ٦٠، أي يمكن أن تكون مجموع الرؤوس الملتقية ٣٦٠°

يمكن استعمال مثلثات متطابقة الأضلاع.