حدد ما إذا كان كلّ زوج من الزوايا الآتية متكاملة أو متتامّة أو غير ذلك.

مجموع الزاويتين ٧٥ + ١٥ = ٩٠$°$

إذا الزاويتان متتامتان.

حل اسئلة تحقق من فهمك

هندسة: استعن بالزاوية المرسومة جانباً في كل من الأسئلة الآتية:

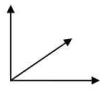
١) صنف $\angle$أ على أنها زاوية حادة أو قائمة أو منفرجة أو مستقيمة.

U قياسها يساوي ٩٠°

إذاً هي زاوية قائمة.

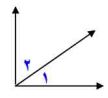
٢) انسخ $\angle$أ على ورقة ثم ارسم نصف مستقيم يقسمها إلى زاويتين متطابقتين وسمها $\angle$١ و $\angle$٢

٣) ما قياس كل من $\angle$١ و $\angle$٢؟

قياس U ١ وU ٢ متساوي.

= ٩٠ $÷$ ٢ = ٤٥°

٤) ما مجموع قياس $\angle$١ و $\angle$٢؟

مجموع قياس U ١ وU ٢ يساوي قياس الزاوية الرئيسية = ٩٠°

٥) انسخ $\angle$أ على ورقة ثم ارسم نصف مستقيم يقسمها إلى زاويتين غير متطابقتين وسمِّهما $\angle$٣ و $\angle$٤.

٦) ماذا تلاحظ على مجموع قياس الزاويتين $\angle$٣ و $\angle$٤؟

مجموع قياس الزاويتين U ٣ وU ٤ يساوي ٩٠°

٧) أجب عن الأسئلة من ١ - ٦ مستعملاً $\angle$ب المجاورة.

بما أن قياس الزاوية يساوي ١٨٠° إذن الزاوية مستقيمة.

قياس كل من ومتساوي U ١ وU ٢ يساوي نصف الزاوية المستقيمة ١٨٠ ÷ ٢ = ٩٠°

مجموع قياس U ١ وU ٢ يساوي ١٨٠°

مجموع قياس الزاويتين U ٣ وU ٤ يساوي ١٨٠°

حدد ما إذا كان كل زوج من الزوايا الآتية متكاملة أو متتامة أو غير ذلك.

أ)

مجموع الزاويتين ٩٠ + ٨٥ = ١٧٥°

إذا ليست متكاملة ولا متتامة.

ب)

مجموع الزاويتين ٧٥ + ١٥ = ٩٠°

إذا الزاويتان متتامتان.

ج) جبر: أوجد قيمة س.

بما أن الزاويتان متكاملتان، إذاً مجموعهما يساوي ١٨٠°

٤٦ + س = ١٨٠° بطرح ٤٦ من الطرفين.

س = ١٣٤°

د) جبر: إذا كانت $\angle$ ل و $\angle$ م متتامتين وكان ق$\angle$م = ٦٥° فما ق$\angle$ ل؟

بما أن U م متتامتيّن، وكان ق U م = ٦٥°

U ل + U م = ٩٠°

U ل + ٦٥ = ٩٠

U ل = ٢٥°