ما قياس الزاوية المجهولة في المثلث الموضّح في هيكل الدّراجة؟

بما أن مجموع قياسات زوايا المثلث = ١٨٠$°$

قياس الزاوية المجهولة في المثلث:

س + ٨٩ + ٦٠ = ١٨٠$°$ اجمع الزاويتين.

س + ١٤٩ = ١٨٠ اطرح ١٤٩ من الطرفين.

س = ٣١$°$

الإجابة هي: ه)

حل اسئلة تحقق من فهمك

١) ما نوع الزاوية التي تشكلت من تجاور الزوايا الثلاث؟

زاوية مستقيمة.

٢) كرر النشاط مع مثلث آخر، ثم استنتج قاعدة عن مجموع قياسات زوايا أي مثلث.

ارسم مثلثاً بثلاث زوايا حادة سم الزوايا د، ه، و، ثم قص المثلث.

اطو د، ه، وبحيث تلتقي رؤوسها عند نقطة على المستقيم بين U د وU و

نستنتج من ذلك أن مجموع قياسات زوايا المثلث الداخلة =١٨٠°

أ) جبر: في $△$ أ ب ج إذا كان ق$\angle$أ = ٢٥° و ق$\angle$ب = ١٨٠° فأوجد ق$\angle$ج.

بما أن مجموع قياسات زوايا المثلث = ١٨٠°

ق U ج + ٢٥ + ١٠٨ = ١٨٠ اجمع الزاويتين.

ق U ج + ١٣٣ = ١٨٠° اطرح ١٣٣ من الطرفين.

ق U ج = ٤٧°

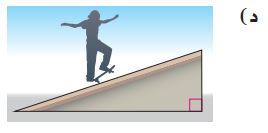
ب) ما قياس الزاوية المجهولة في المثلث الموضح في هيكل الدراجة؟

هـ) ٣١°

ز) ٤٥°

و) ٤٠°

ح) ٥٠°

بما أن مجموع قياسات زوايا المثلث = ١٨٠°

قياس الزاوية المجهولة في المثلث:

س + ٨٩ + ٦٠ = ١٨٠° اجمع الزاويتين.

س + ١٤٩ = ١٨٠ اطرح ١٤٩ من الطرفين.

س = ٣١°

الإجابة هي: هـ)

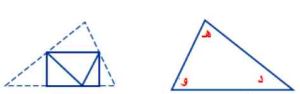
جـ) صنف المثلث المشار إليه في كل من الصورتين أدناه باستعمال الزوايا والأضلاع:

ج) بما أن المثلث به زاوية قائمة وضلعين متطابقين، إذاً المثلث قائم الزاوية ومتطابق الضلعين.

د) بما أن المثلث به زاوية قائمة وأضلاعه مختلفة الأطوال، إذاً المثلث قائم ومختلف الأضلاع.

ارسم مثلثاً في كل من الحالتين الآتيتين ثم صنفه:

هـ ) مثلث فيه ثلاث زوايا حادة، وثلاثة أضلاع متطابقة.

ارسم ضلع من المثلث، ثم ارسم ضلعين بنفس الطول.

المثلث حاد الزوايا ومتساوي الأضلاع.

و) مثلث فيه زاوية واحدة قائمة ولا يوجد فيه أضلاع متطابقة.

ارسم زاوية قائمة لها ضلعان غير متساويين، وصل بين طرفي الضلعين لعمل المثلث، مثلث قائم الزاوية، مختلف الأضلاع.