حلول الأسئلة
السؤال
أوجد قيمة س في كل من مثلث مما يـأتي:
الحل
بما أن مجموع زوايا المثلث يساوي ١٨٠
٢ س + س + ٩٠ = ١٨٠
٣ س + ٩٠ = ١٨٠ بطرح ٩٠ من الطرفين.
٣ س = ٩٠ بقسمة الطرفين على ٣
س = ٣٠
شاهد حلول جميع الاسئلة
حل اسئلة تدرب وحل المسائل
١١) .JPG)
بما أن مجموع زوايا المثلث = ١٨٠°
س + ٣٣ + ٢٩ = ١٨٠° اجمع الزاويتين.
س + ٦٢ = ١٨٠° اطرح ٦٢ من الطرفين.
س = ١١٨°
١٢) .JPG)
بما أن مجموع زوايا المثلث = ١٨٠°
س + ٥٦ + ٣٤ = ١٨٠° اجمع الزاويتين.
س + ٩٠ = ١٨٠° اطرح ٩٠ من الطرفين.
س = ٩٠°
١٣) 
بما أن مجموع زوايا المثلث = ١٨٠°
س + ٥٣ + ٩٠ = ١٨٠° اجمع الزاويتين.
س + ١٤٣ = ١٨٠° اطرح ١٤٣ من الطرفين.
س = ٣٧°
١٤) جبر: أوجد قك في ك ر س إذا كان قر = ٢٥° و قس = ١٠٢°.
بما أن مجموع زوايا المثلث يساوي ١٨٠°
U ك + U ر + U س = ١٨٠°
U ك + ٢٥ + ١٠٢ = ١٨٠ بجمع الزاويتين.
U ك + ١٢٧ = ١٨٠ بطرح ١٢٧ من الطرفين.
U ك = ٥٣°
١٥) عمارة: ما نوع المثلث المشار إليه في صورة سقف مطار الملك خالد الدولي المجاورة؟ هل هو مثلث حاد الزوايا أم قائم الزاوية أم منفرج الزاوية؟
المثلث قائم الزاوية.
صنف المثلث المشار إليه في كل من الأشكال الآتية من حيث الزوايا والأضلاع:
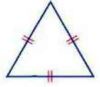
١٦) بما أن جميع زوايا المثلث أقل من ٩٠° وأطوال أضلاعه متساوية؛ إذاً المثلث حاد الزوايا ومتطابق الأضلاع.
١٧) بما أن جميع زوايا المثلث أقل من ٩٠° وأطوال أضلاعه متساوية؛ إذاً المثلث حاد الزوايا ومتطابق الأضلاع.
١٨) بما أن المثلث به زاوية منفرجة، وضلعين متساويين المثلث منفرج الزاوية ومتطابق الضلعين.
١٩) بما أن جميع زوايا المثلث أقل من ٩٠° وبه ضلعين متساويين إذاً المثلث حاد الزوايا ومتطابق الضلعيين.
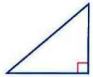
٢٠) بما أن به زاوية قائمة وضلعين متساويين إذاً المثلث قائم الزاوية متطابق الضلعين.
٢١) بما أن به زاوية قائمة، أطوال أضلاعه مختلفة إذاً المثلث قائم الزاوية مختلف الأضلاع.
رسم المثلثات: للأسئلة ٢٢ - ٢٥ الاسم مثلثاً ثم صنفه:
٢٢) مثلث مختلف الأضلاع وزواياه حادة.
ارسم زاوية حادة بضلعين مختلفين في الطول ثم صل بين طرفي الضلعين. مثلث حاد الزوايا ومختلف الأضلاع.
٢٣) مثلث متطابق الضلعين ومنفرج الزاوية.
نرسم زاوية منفرجة ضلعيها متساويين ثم صل بين طرفي الضلعين. مثلث منفرج الزاوية متطابق الضلعين.
٢٤) مثلث متطابق الأضلاع وزواياه حادة.
ارسم زاوية حادة ضلعيها متساوي وارسم ضلع ثالث نفس الطول مثلث حاد الزوايا ومتطابق الأضلاع.
٢٥) مثلث قائم الزاوية ومختلف الأضلاع.
مثلث قائم الزاوية ومختلف الأضلاع.
أوجد قياس الزاوية المجهول في كل من المثلثات الآتية:
٢٦) ٨٠° ، ٢٠,٥، س°
بما أن مجموع زوايا المثلث يساوي ١٨٠
س + ٨٠ + ٢٠,٥ = ١٨٠ بجمع الزاويتين.
س + ١٠٠,٥ = ١٨٠ بطرح ١٠٠,٥ من الطرفين.
س = ٧٩,٥
٢٧) ٥٧، س، ٥٠,٢
بما أن مجموع زوايا المثلث يساوي ١٨٠°
س + ٧٥ + ٥٠,٢ = ١٨٠ بجمع الزاويتين.
س + ١٢٥,٥ = ١٨٠ بطرح ١٢٥,٥ من الطرفين.
س = ٥٤,٥°
٢٨) ١١٠،٢، س، ٣٥,٦
بما أن مجموع زوايا المثلث يساوي ١٨٠°
س + ٣٥,٦ + ١١٠,٢ = ١٨٠ بجمع الزاويتين.
س + ١٤٥,٨ = ١٨٠ بطرح ١٤٥,٨ من الطرفين.
س = ٣٤,٢°
الجبر: أوجد قيمة س في كل من مثلث مما يـأتي:
٢٩) .JPG)
بما أن مجموع زوايا المثلث يساوي ١٨٠°
س + س + س = ١٨٠
٣ س = ١٨٠ بقسمة الطرفين على ٣
س = ٦٠°
٣٠) .JPG)
بما أن مجموع زوايا المثلث يساوي ١٨٠°
٢ س + س + ٩٠ = ١٨٠
٣ س + ٩٠ = ١٨٠ بطرح ٩٠ من الطرفين.
٣ س = ٩٠° بقسمة الطرفين على ٣
س = ٣٠°
٣١) .JPG)
بما أن مجموع زوايا المثلث يساوي ١٨٠°
س + س + ٢٥ = ١٨٠
٢ س + ٢٥ = ١٨٠ بطرح ٢٥ من الطرفين.
٢ س = ١٥٥ بقسمة الطرفين على ٢
س = ٧٧,٥°

.JPG)

.JPG)

.JPG)
.JPG)
.JPG)
.JPG)