أوجد قياس الزاوية المجهولة في كل شكل رباعي مما يأتي:

بما أن مجموع زوايا الشكل الرباعي = ٣٦٠°

١٠٦ + ٦٧ + ١٣١ + س = ٣٦٠ بجمع الثلاث زوايا.

٣٠٤ + س = ٣٦٠ بطرح ٣٠٤ من الطرفين.

س = ٥٦$°$

حل اسئلة تدرب وحل المسائل

صنف كل شكل رباعي مما يأتي بأفضل اسم يصفه:

٩)

بما أن جميع زواياه قائمة وجميع أضلاعه متساوية إذاً الشكل مربع.

١٠)

بما أن في الشكل ضلعين متوازيين إذاً الشكل شبه منحرف.

١١)

بما أن كل ضلعين متجاورين متساويين فقط إذاً الشكل رباعي.

١٢)

بما أن جميع أضلاعه متساوية إذاً الشكل معين.

١٣)

بما أن بالشكل زاويتين قائمتين وضلعين متوازيين.

١٤)

بما أن كل ضلعين متقابلين متساويين متوازيين إذاً الشكل متوازي أضلاع.

جبر: أوجد قياس الزاوية المجهولة في كل شكل رباعي مما يأتي:

١٥)

بما أن مجموع زوايا الشكل الرباعي = ٣٦٠°

١٠٦ + ٦٧ + ١٣١ + س = ٣٦٠ بجمع الثلاث زوايا.

٣٠٤ + س = ٣٦٠ بطرح ٣٠٤ من الطرفين.

س = ٥٦°

١٦)

بما أن مجموع زوايا الشكل الرباعي = ٣٦٠$°$

٨٠ + ٨٩ + ٧٢ + س = ٣٦٠ بجمع الثلاث زوايا

٢٤١ + س = ٣٦٠ بطرح ٢٤١ من الطرفين

س = ١١٩$°$

١٧)

بما أن مجموع زوايا الشكل الرباعي = ٣٦٠$°$

٩٠ + ٩٠ + ١١٣ + س = ٣٦٠ بجمع الثلاث زوايا.

٢٩٣ + س = ٣٦٠ بطرح ٢٩٣ من الطرفين.

س = ٦٧$°$

١٨) جبر: أوجد ق$\angle$ب في الشكل الرباعي أ ب ج د إذا كان ق$\angle$أ = ٨٧°، و ق$\angle$ج = ١٣٥°، و ق$\angle$د =٢٢°.

بما أن مجموع زوايا الشكل الرباعي= ٣٦٠°

U أ + U ب + U ج + U د = ٣٦٠

٧٨ + U ب + ١٣٥ + ٢٢ = ٣٦٠ بجمع الثلاث زوايا.

٢٤٤ + U ب = ٣٦٠ بطرح ٢٤٤ من الطرفين.

U ب = ١١٦°

١٩) جبر: أوجد ق$\angle$ص في الشكل الرباعي س ص ع ل، إذا كان ق$\angle$س = ٤٥° و ق$\angle$ع = ١٢٨° و$\angle$ل قائمة.

بما أن مجموع زوايا الشكل الرباعي= ٣٦٠$°$

U س + U ص + U ع + U ل = ٣٦٠

U ص + ٤٥ + ١٢٨ + ٩٠ = ٣٦٠ بجمع الثلاث زوايا.

U ص + ٢٦٣ = ٣٦٠ بطرح ٢٦٣ من الطرفين.

U ص =٩٧°

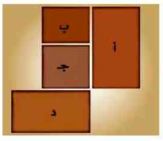
٢٠) تصميم: حدد أشكال البلاطات المستعملة في التصميم المجاور واستعمل أفضل اسم لوصف كل منها.

أ، ب، د مستطيل.

ج مربع.

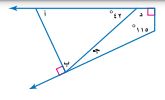
٢ ١) قياس: أوجد قياس الزوايا المجهولة أ، ب، جـ، د في الشكل المجاور ووضح ذلك.

بما أن µ د والزاوية المجاورة متكاملتان.

µ د + ٤٢ = ١٨٠ (بطرح ٤٢ من الطرفين)

µ د = ١٣٨°

بما أن مجموع زوايا الشكل المربع = ٣٦٠°

١١٥ + ٩٠ + ١٣٨ + µ جـ =٣٦٠ (بجمع الثلاث زوايا)

µ جـ + ٣٤٣ = ٣٦٠ (بطرح ٣٤٣ من الطرفين)

جـ = ١٧°

بما أن µ ب وµ جـ متتامتان

µ ب + µ جـ = ٩٠ (بطرح ١٧ من الطرفين)

µ ب = ٧٣°

بما أن مجموع زوايا المثلث = ١٨٠ (بجمع الزاويتين)

µ أ + ١١٥ = ١٨٠ (بطرح ١١٥ من الطرفين)

µ أ = ٦٥°

أوجد قياس الزوايا المجهولة في كل من الأشكال الرباعية:

٢٢) ٥, ٣٧°، ٧٨°، ٤, ١١٥°، س°

بما أن مجموع زوايا الشكل المربع = ٣٦٠°

٣٧,٥ + ٧٨ + ١١٥,٤ + س = ٣٦٠ (بجمع الثلاث زوايا)

١٣٠,٩ + س = ٣٦٠ (بطرح ١٣٠,٩ من الطرفين).

س = ١٢٩,١

٢٣) ٢٥,٥°، س°، ٩, ١٦٥°، ٣٦,٨°

بما أن مجموع زوايا الشكل المربع = ٣٦٠°

٢٥,٥ + س + ١٦٥,٩ + ٣٦,٨ = ٣٦٠ (بجمع الثلاث زوايا)

٢٢٨,٢ + س =٣٦٠ (بطرح ٢٢٨,٢ من الطرفين)

س = ١٣١,٨

جبر: أوجد قيمة س في كل من الأشكال الرباعية الآتية:

٢٤)

بما أن مجموع زوايا الشكل المربع = ٣٦٠°

٢س + ٢س + ٢س + ٢س = ٣٦٠

٨س = ٣٦٠

س = ٤٥°

٢٥)

بما أن مجموع زوايا الشكل المربع = ٣٦٠°

١٣٥ + ١٣٥ + س + س= ٣٦٠ (بجمع الحدود المتشابهة)

٢٧٠ + ٢س = ٣٦٠ (بطرح ٢٧٠ من الطرفين)

٢س = ٩٠ بقسمة الطرفين على ٢

س = ٤٥°

٢٦)

١٠٠ + ١٠٠ + س + س = ٣٦٠ (بجمع الحدود المتشابهة)

٢٠٠ + ٢س = ٣٦٠ (بطرح ٢٠٠ من الطرفين)

٢س = ١٦٠ بقسمة الطرفين على ٢

س = ٨٠

فن: للأسئلة ٢٧ - ٢٩: حدد أنواع المثلثات والأشكال الرباعية المستعملة في كل شكل واستعمل أفضل اسم لوصفها.

٢٧)

مربع، مثلث متطابق الأضلاع، مثلث مختلف الأضلاع، شبه منحرف.

٢٨)

مربع، مستطيل، مثلث قائم الزاوية متطابق الضلعين.

٢٩)

مربع، شبه منحرف، مثلث قائم الزاوية متطابق الضلعين.

تحد: لحل السؤالين ٣٠ - ٣١، ارجع للجدول أدناه الذي يبين خصائص عدة متوازيات أضلاع الخاصية أ تعني أن كل زوج من الأضلاع المتقابلة متوازية ومتقابلة.

٣٠) إذا كانت الخاصية جـ تعني أن الأضلاع الأربعة متطابقة فصنف متوازيات الأضلاع ١ و٢ و٣ ووضح إجابتك.

• متوازي الأضلاع ١: معين.
• متوازي الأضلاع ٢: مربع.
• متوازي الأضلاع ٣: متوازي الأضلاع.

٣١) إذا كان متوازي الأضلاع ٣ مستطيلاً فصنف الخاصية ب وضح إجابتك.

الخاصية ب: أن جميع زواياه قائمة.

لأن متوازي الأضلاع والمستطيل مشتركين في أن كل ضلعين متقابلين متوازيين ومتطابقين؛ ولكن المستطيل يختلف في أن زواياه قائمة.

تبرير: حدد ما إذا كانت كل عبارة مما يأتي صحيحة أم أحياناً أم غير صحيحة أبداً.

٣٢) الشكل الرباعي هو شبه منحرف

صحيحة أحياناً، لأن الشكل الرباعي يمكن أن يكون مستطيلاً أيضاً

٣٣) شبه المنحرف هو متوازي أضلاع

خطأ، في شبه المنحرف زوج واحد فقط من الأضلاع المتو ازية وفي متوازي الأضلاع زوجان من الأضلاع المتوازية

٣٤) المربع هو مستطيل

صحيحة دائماً، له جميع خصائص المستطيل.

٣٥) المعين هو مربع

صحيحة أحياناً، يكون المعين إذا كانت زواياه الأربع قوائم.

٣٦) اكتشف الخطأ: وصف كل من فيصل وعبد العزيز المستطيل فمن وصفه أدق؟

وصف عبد العزيز أدق لأن الزوايا القائمة هي التي تميز المستطيل عن متوازي الأضلاع.

٣٧) اكتب: إذا كان قطرا المستطيل متطابقين وقطرا المعين متعامدين فما الذي نستنتجه عن قطري كل من المربع ومتوازي الأضلاع؟ وضح إجابتك.

استنتج أن قطر المربع متعامدين مثل المعين لأن كلاهما أضلاعه متطابق واستنتج أن قطرا متوازي الأضلاع مثل المستطيل كل ضلعين متقابلين متوازيين ومتطابقين.

٣٨) أي الأسماء الآتية لا يصف الشكل أدناه؟

أ. مربع

ب. مستطيل

جـ. معين

د. شبه منحرف

٣٩- أي الجمل الآتية صحيحة دائماً بالنسبة للمعين؟

أ. له أربع زوايا قائمة

ب. مجموع زواياه متقابلان متوازيان فقط

جـ. فيه ضلعان متقابلان متوازيان فقط

د. له أربعة أضلاع متطابقة.