صنف كلاً من الشكلين الرباعيين الآتيين:

• الشكل الأول أضلاع الشكل المتقابلة متناظرة، جميع زواياه قوائم، أضلاعه المتقابلة متوازية، إذن الشكل مستطيل.
• الشكل الثاني: جميع أضلعه متطابقة، جميع زواياه قوائم، أضلاعه المتقابلة متوازية، إذن الشكل مربع.

حل أسئلة تأكد

أوجد قيمة س في كل من الشكلين الرباعيين الآتيين:

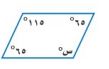
١-

س + ١٠٥ + ٦٠ + ١٢٠ = ٣٦٠°

س = ٣٦٠ - ٢٨٥ = ٧٥°

٢-

س + ١٠٧ + ٦٣ + ٥٨ = ٣٦٠°

س = ٣٦٠ - ٢٢٨ = ١٣٢°

٣- صنف كلاً من الشكلين الرباعيين الآتيين:

الشكل الأول أضلاع الشكل المتقابلة متناظرة، جميع زواياه قوائم، أضلاعه المتقابلة متوازية، إذن الشكل مستطيل.

الشكل الثاني: جميع أضلعه متطابقة، جميع زواياه قوائم، أضلاعه المتقابلة متوازية، إذن الشكل مربع.

٤- إجابة قصير: أوجد قيمة س في متوازي الأضلاع المجاور.

س + ١١٥ + ٦٥ + ٦٥ = ٣٦٠°

س = ٣٦٠ - ٢٤٥ = ١١٥°