صنف كلاً من المثلثين الآتيين إلى: متتامتين، أو متكاملتين، أو غير ذلك:

متتامتان، فمجموع قياس الزاويتين يساوي ٩٠°

حل أسئلة اختبار الفصل التاسع

استعمل المنقلة لقياس الزوايا الآتية وصنفها إلى حادة، أو منفرجة، أو قائمة، أو مستقيمة:

١-

٩٠° زاوية قائمة.

٢-

١٧° زاوية حادة.

٣-

١٨٠° زاوية مستقيمة.

٤- تلال: قدر قياس س في الصورة المجاورة.

١٥° تقريباً، لأنها زاوية حادة.

صنف كلاً من المثلثين الآتيين إلى: متتامتين، أو متكاملتين، أو غير ذلك:

٥-

متكاملتان، فمجموع قياس الزاويتين يساوي ٩٠°

٦-

متتامتان، فمجموع قياس الزاويتين يساوي ٩٠°

صنف كلاً من المثلثين الآتيين إلى: مختلف الأضلاع، أو متطابق الضلعين، أو متطابق الأضلاع:

٧-

جميع الأضلاع متطابقة، إذن المثلث متطابق الأضلاع.

٨-

يوجد ضلعين متطابقين، إذن المثلث متطابق الضلعين.

٩- أوجد قيمة س في المثلث المجاور.

س + ٢٣ + ٣٤ = ١٨٠°

س = ١٨٠ - (٢٣ + ٣٤) = ١٨٠ - ٥٧ = ١٢٣°

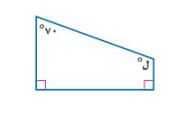
١٠- اختيار من متعدد: أوجد ق $\angle$ل في شبه المنحرف المجاور.

أ. ١١٠°

ب. ١٠٠°

جـ. ٩٠°

د. ٢٠°

ل + ٩٠ + ٩٠ + ٧٠ = ٣٦٠°

ل = ٣٦٠ - ٢٥٠ = ١١٠°

إذن الإجابة الصحيحة هي: أ ١١٠°

١١- حدائق: صنف كلاً من الشكلين الرباعيين المبينين في الصورة أدناه.

الشكل أ جميع أضلاعه متطابقة، أضلاعه المتقابلة متوازية.

إذن الشكل مربع.

الشكل ب أضلاع الشكل المتقابلة متناظرة، جميع زواياه قوائم، أضلاعه المتقابلة متوازية.

إذن الشكل مستطيل.

١٢- اختيار من متعدد: أي من العبارات الآتية غير صحيحة بناء على الأشكال أدناه؟

أ. جميع الأشكال رباعية.

ب. كل شكل من هذه الأشكال مضلع.

جـ. كل شكل من هذه الأشكال متوازي أضلاع.

د. مجموع قياسات زوايا كل من هذه الأشكال يساوي ٣٦٠°

الشكل ليس متوازي أضلاع،

إذن الإجابة الصحيحة هي:

جـ. كل شكل من هذه الأشكال متوازي أضلاع.

١٣- رياضة: يخطط جاسم لاستعمال مخاريط برتقالية اللون لتعيين حدود ملعب مستطيل الشكل وسيضع على كل ضلع ٥ مخاريط من ضمنها مخروط واحد عند كل من أركان الملعب فما عدد المخاريط اللازمة لذلك؟

أفهم: معطيات المسألة: الملعب مستطيل الشكل.

يضع على كل ضلع ٥ مخاريط من ضمنها مخروط واحد عند كل ركن.

المطلوب: عدد المخاريط اللازمة لذلك.

خطط: باستعمال خطة رسم صورة أو أرسم صورة لأجد حل المسألة.

حل: عند رسم صورة أجد أن كل ضلع من المستطيل عليه ٣ مخاريط.

إلى جانب مخروط عند كل ركن.

(٣ × ٤) + ٤ = ١٦

أعد المخاريط أجد أنه يضع ١٦ مخروطاً حول الملعب.

تحقق: تحقق من المخطط، إذن الإجابة صحيحة.