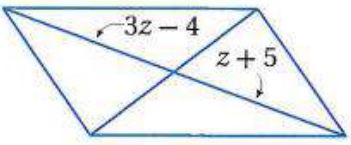
أوجد قيمة المتغير في كل من متوازيي الأضلاع الآتيين:

الحل: (تعريف تطابق القطع المستقيمة).

تحقق من فهمك

1) مرايا: تستعمل في مرآة الحائط جانباً متوازيات أضلاع يتغير شكلها كلما مد الذراع في JKLM إذا كان MJ=8cm، فأوجد كلاً مما يأتي:

.

الحل: LK =MJ =8 cm (كل ضلعين في متوازي الأضلاع متطابقان).

الحل:

(كل زاويتين متقابلتين في متوازي الأضلاع متطابقان).

c) إذا مد الذراع حتى أصبح فكم يصبح قياس كل من برر اجابتك.

الحل: سيكون قياس كل من الزوايا الأخرى 90º تبعاً للنظرية 1.6

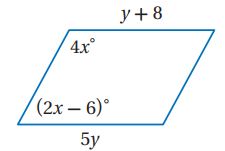
أوجد قيمة المتغير في كل من متوازيي الأضلاع الآتيين:

2A)

الحل: (تعريف تطابق القطع المستقيمة).

2B)

الحل: (قطرا متوازي الأضلاع ينصف كلاً منهما الآخر).

3) هندسة احداثيات: أوجد إحداثيي نقطة تقاطع قطري RSTU الذي رؤوسه

الحل: بما أن قطري متوازي الأضلاع ينصف كلاً منهما الآخر فإن نقطة تقاطعهما هي نقطة منتصف كل من أوجد نقطة منتصف التي طرفاها

(صيغة نقطة المنتصف).

(بالتبسيط).

إذن إحداثيات نقطة تقاطع قطري RSTU هما .

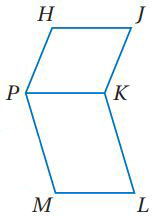
4) اكتب برهاناً ذا عمودين:

المعطيات: HJKP، PKLM

المطلوب:

الحل:

المعطيات: متوازي الأضلاع HJKP، PKLM

المطلوب:

البرهان:

العبارات (المبررات):

1)متوازي أضلاع (معطيات).

2) (الأضلاع المتقابلة في متوازي الأضلاع متطابقة).

3) (خاصية التعدي).