حلول الأسئلة
السؤال
ليكن د(س) = ٢س٢ - ٤س - ١.
حدد فيما إذا كان للدالة قيمة عظمى أم قيمة صغرى.
الحل
قيمة صغرى لأن أ = ٢ وهي قيمة موجبة إذن المنحنى مفتوح للأعلى.
شاهد حلول جميع الاسئلة
حل أسئلة تحقق من فهمك
١) استعمل جدول القيم لتمثيل الدالة ص = س٢ + ٣ بيانياً، وحدد مجالها ومداها.
| س | -٢ | -١ | ٠ | ١ | ٢ |
| ص | ٧ | ٤ | ٣ | ٤ | ٧ |
المجال = مجموعة الأعداد الحقيقية.
المدى = {ص | ص ٣}
٢أ) .JPG)
الرأس = (-١، ٣)،
محور التماثل س = ١،
المقطع الصادي = ٢.
٢ب) .JPG)
الرأس = (١، ٣)،
محور التماثل س = ١،
المقطع الصادي = ٤.
٣أ) ص = -٣س٢ + ٦س - ٥
س =
س = = ١
معادلة محور التماثل هي س = ١
عند س = ١
ص = -٣ + ٦ - ٥ = -٢
إذن الرأس هي (١، -٢)
وبما أن المقطع الصادي هو عند النقطة (٠، جـ) إذن المقطع الصادي هو - ٥.
٣ب) ص = ٢س٢ + ٢س + ٢
س =
س =
معادلة محور التماثل هي س = -
عند س =
ص = ٢× -٢ × + ٢ =
إذن الرأس هي (-، )
وبما أن المقطع الصادي هو عند النقطة (٠، جـ) إذن المقطع الصادي هو ٢.
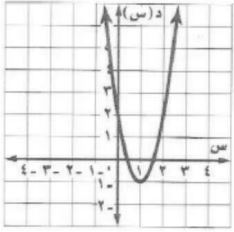
ليكن د(س) = ٢س٢ - ٤س - ١,
٤أ) حدد فيما إذا كان للدالة قيمة عظمى أم قيمة صغرى.
قيمة صغرى لأن أ = ٢ وهي قيمة موجبة إذن المنحنى مفتوح للأعلى.
٤ب) أوجد القيمة العظمى أو القيمة الصغرى للدالة.
القيمة الصغرى هي -٣
س =
= = ١
ص = ٢- ٤ - ١ = -٣
٤جـ) حدد مجال الدالة ومداها.
المجال = مجموعة الأعداد الحقيقة
المدى = {ص| ص -٣}
٥أ) د(س) = -٢س٢ +٢س - ١
س =
س =
معادلة محور التماثل هي س =
عند س =
ص = -٢ × + ٢ × - ١ = -
إذن الرأس هي (، -)
وبما أن أ قيمة سالبة فالتمثيل مفتوح لأسفل لذا الرأس تمثيل قيمة عظمى والمقطع الصادي هو قيمة جـ = -١.
٥ب) د(س) = ٣س - ٦س + ٢
س =
س = = ١
معادلة محور التماثل هي س = ١
عند س = ١
ص = ٣ - ٦ + ٢ = -١
إذن الرأس هي (١، -١)
وبما أن أ قيمة موجبة فالتمثيل مفتوح لأعلى لذا الرأس تمثيل قيمة صغرى والمقطع الصادي هو قيمة جـ = ٢.
٦) رمي الرمح: يشارك علي في مسابقة رمي الرمح، ويمكن تمثيل ارتفاع الرمح (ص) بالأقدام بعد (س) ثانية، بالمعادلة ص = -١٦س + ٦٤س + ٦.
أ) مثل مسار هذا الرمح بيانياً.
س =
س = = ٢
معادلة محور التماثل هي س = ٢
عند س = ٢
ص = -١٦ × ٤ + ٦٤ × ٢ + ٦ = ٧٠
إذن الرأس هي (٢، ٧٠)
وبما أن أ قيمة سالبة فالتمثيل مفتوح لأسفل لذا الرأس تمثل قيمة عظمى والمقطع الصادي هو قيمة جـ = ٦.
ب) ما الارتفاع الذي أطلق منه الرمح؟
٦ أقدام.
جـ) ما أقصى ارتفاع يصله الرمح؟
٧٠ قدم.


.JPG)
.JPG)
.JPG)
.JPG)