حلول الأسئلة
السؤال
قسم قصي ٢١ تفاحة مجموعتين، إذا كان عدد التفاح في المجموعة الأولى يزيد ٥ تفاحاتٍ عن عدد التفاح في المجموعة الثانية، فكم تفاحة في المجموعة الثانية؟ (الدرس ١١-٢)
الحل
- المجموعة الأولى + (المجموعة الثانية + ٥) = ٢١
- المجموعة الأولى + المجموعة الثانية = ٢١ - ٥ = ١٦
- المجموعة الأولى = ١٣
- المجموعة الثانية = ٨
شاهد حلول جميع الاسئلة
حل أسئلة اختبار منتصف الفصل
في كل من الشكلين الآتيين، اذكر اسم الشكل لفظياً وبالرمز: (الدرس١١-١)
١) .JPG)
ج د
٢) 
المستوى م ل ن
قس طول القطعة المستقيمة، ثم بين إذا كانت القطعتان متطابقتان أم لا. اكتب نعم أو لا. (الدرس ١١-١)
٣) .JPG)
نعم
٤) .JPG)
لا.
٥) قسم قصي ٢١ تفاحة مجموعتين، إذا كان عدد التفاح في المجموعة الأولى يزيد ٥ تفاحاتٍ عن عدد التفاح في المجموعة الثانية، فكم تفاحة في المجموعة الثانية؟ (الدرس ١١-٢)
- المجموعة الأولى + (المجموعة الثانية + ٥) = ٢١
- المجموعة الأولى + المجموعة الثانية = ٢١ - ٥ = ١٦
- المجموعة الأولى = ١٣
- المجموعة الثانية = ٨
٦) إذا كان مجموع زوايا المضلع أدناه ٥٤٠ درجة، فما قياس كل زاويةٍ، إذا كانت جميع زواياه متطابقة؟ (الدرس ١١-٢)
عدد زوايا المضلع ٥ زوايا بما أن جميع الزوايا متساوية.
قياس كل زاوية =
٧) اختيارٌ من متعدد: أي الأشكال الآتية يحوي ضلعين متوازيين فقط؟ (الدرس ١١-٣)
- مستطيل.
- مربع.
- شبه منحرف.
- متوازي أضلاع.
أوجد عدد الزوايا الحادة في كل شكل مما يأتي: (الدرس١١-٣)
٨) 
لا يوجد.
٩) 
زاويتان.
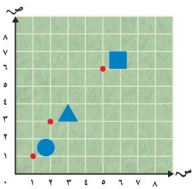
استعمل الخريطة أدناه لتحدد موقع كل مما يأتي: (الدرس١١ -٤)
١٠) المربع.
المربع (٦،٥).
١١) المثلث.
المثلث (٣،٢).
١٢) الدائرة.
الدائرة (١،١).
١٣) .JPG) هل يمكن اعتبار متوازي الأضلاع شبه منحرف؟ ولماذا؟ (الدرس ١١-٣)
هل يمكن اعتبار متوازي الأضلاع شبه منحرف؟ ولماذا؟ (الدرس ١١-٣)
لا، لأن متوازي الأضلاع كل ضلعين متقابلين متوازيين، أما شبه المنحرف يوجد به ضلعين متقابلين فقط متوازيين والضلعين الآخرين غير متوازيين.


.JPG)