اكتب معادلة لإيجاد طول الضلع المجهول في كل مثلث قائم الزاوية طول وتره جـ، ثم أوجد الطول المجهول، وقرب الناتج إلى أقرب جزء من عشرة إذا لزم ذلك:

أ = ٤٨م، ب = ٥٥م

ج^٢ = أ^٢ + ب^٢

^٢٩,٤ = أ^٢ + ^٢٤,٥

أ^٢ = ^٢٩,٤ - ^٢٤,٥

أ^٢ = ٦٨,١١

أ = ٨,٢٥ م.

 ب = ٤,٥م، جـ ٩,٤م

ج^٢ = أ^٢ + ب^٢

^٢٩,٤ = أ^٢ + ^٢٤,٥

أ^٢ = ^٢٩,٤ - ^٢٤,٥

أ^٢ = ٦٨,١١

أ = ٨,٢٥ م.

حل أسئلة تدرب وحل المسائل

اكتب معادلة لإيجاد الضلع المجهول في كل مثلث قائم الزاوية، ثم قرب طول الضلع المجهول إلى أقرب جزء من عشرة إذا لزم ذلك:

٨)

ج^٢ = أ^٢ + ب^٢

ج^٢ = ^٢٣٦ +^٢٢٧

ج^٢ = ١٢٩٦ + ٧٢٩ = ٢٠٢٥

ج = $\sqrt{\mathrm{٢٠٢٥}}$

ج= ٤٥ م.

٩)

ج^٢ = أ^٢ + ب^٢

ج^٢ = ^٢١٢ + ^٢٥

ج^٢ = ١٤٤ + ٢٥ = ١٦٩

ج = $\sqrt{\mathrm{١٦٩}}$

ج= ١٣ ملم.

١٠)

ج^٢ = أ^٢ + ب^٢

^٢١٥ = أ^٢ + ^٢١٠

أ^٢ = ^٢١٥ - ^٢١٠

أ^٢ = ٢٢٥ - ١٠٠ = ١٢٥

أ = $\sqrt{\mathrm{١٢٥}}$

ج= ١١,٢ سم.

١١)

ج^٢ = أ^٢ + ب^٢

^٢٦٠ = أ^٢ + ^٢٥١

أ^٢ = ^٢٦٠ - ^٢٥١

أ^٢ = ٣٦٠٠ - ٢٦٠١ = ٩٩٩

أ = $\sqrt{\mathrm{٩٩٩}}$

ج= ٣١,٦ سم.

١٢)

ج^٢ = أ^٢ + ب^٢

^٢٨٠ = ^٢٣٠ + ب^٢

ب^٢ = ^٢٨٠ - ^٢٣٠

ب^٢ = ٦٤٠٠ - ٩٠٠ = ٥٥٠٠

ب = $\sqrt{\mathrm{٥٥٠٠}}$

ب = ٤,٢ ملم.

١٣)

ج^٢ = أ^٢ + ب^٢

^٢١٨ = ^٢٨ + ب^٢

ب^٢ = ^٢١٨ - ^٢٨

ب^٢ = ٣٢٤ - ٦٤ = ٢٦٠

ب = $\sqrt{\mathrm{٢٦٠}}$

ب = ١٦,١م.

حدد ما إذا كان كل مثلث بالأضلاع المعطاة فيما يأتي مثلثاً قائم الزاوية أم لا وتحقق من إجابتك:

١٤) ٢٨م، ١٩٥م، ١٩٧م

ج^٢ = أ^٢ + ب^٢

^٢١٩٧ = ^٢١٩٥ + ^٢٢٨

٣٨٨٠٩ = ٣٨٠٢٥ + ٧٨٤

٣٨٨٠٩ = ٣٨٨٠٩

إذن المثلث قائم الزاوية.

١٥) ٣٠سم، ١٢٢سم، ١٢٥سم

ج^٢ = أ^٢ + ب^٢

^٢١٢٥ = ^٢١٢٢ + ^٢٣٠

١٥٦٢٥ = ١٤٨٨٤ + ٩٠٠

١٥٦٢٥ $\ne$ ١٥٧٨٤

إذن المثلث ليس قائم الزاوية.

١٦) ٢٤م، ١٤٣م، ١٤٥م

ج^٢ = أ^٢ + ب^٢

^٢١٤٥ = ^٢١٤٣ + ^٢٢٤

٢١٠٢٥ = ٢٠٤٤٩ + ٥٧٦

٢١٠٢٥ = ٢١٠٢٥

إذاً المثلث قائم الزاوية.

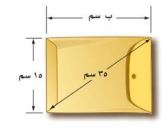
١٧) أجرة بريد: تصنف المغلف بأنه كبير إذا تجاوز طوله ٣٠ سم، هل المغلف المجاور كبير؟

ج^٢ = أ^٢ + ب^٢

^٢٣٥ = ^٢١٥ + ب^٢

ب^٢ = ^٢٣٥ - ^٢١٥

ب^٢ = ١٢٢٥ - ٢٢٥ = ١٠٠٠

ب = $\sqrt{ \mathrm{١٠٠٠} }$

ب > ٣٠

إذاً المغلف كبير.

اكتب معادلة لإيجاد طول الضلع المجهول في كل مثلث قائم الزاوية طول وتره جـ، ثم أوجد الطول المجهول، وقرب الناتج إلى أقرب جزء من عشرة إذا لزم ذلك:

١٨) أ = ٤٨م، ب = ٥٥م

ج^٢ = أ^٢ + ب^٢

^٢٩,٤ = أ^٢ + ^٢٤,٥

أ^٢ = ^٢٩,٤ - ^٢٤,٥

أ^٢ = ٦٨,١١

أ = ٨,٢٥ م.

١٩) ب = ٤,٥م، جـ ٩,٤م

ج^٢ = أ^٢ + ب^٢

^٢٩,٤ = أ^٢ + ^٢٤,٥

أ^٢ = ^٢٩,٤ - ^٢٤,٥

أ^٢ = ٦٨,١١

أ = ٨,٢٥ م.

٢٠) اكتشف الخطأ: يحاول كل من مشعل وإبراهيم أن يجد طول الضلع الثالث في المثلث المجاور أيهما جوابه صحيح؟ فسر إجابتك.

بما أن في المثلث القائم الزاوية حيث جـ طول وتر المثلث، أ، ب طولي ساقي المثلث.

وبما أن طول الوتر = ٤سم؛ المعادلة ^٢٤ = أ^٢ + ^٢٣ فإن إجابة مشعل هي الإجابة الصحيحة.

٢١) تحد: تسمى الأعداد ٣، ٤، ٥ ثلاثية فيثاغورس؛ لأنها تحقق نظرية فيثاغورس أوجد مجموعتين من ثلاثيات فيثاغورس.

١٢، ١٣، ٥

ج^٢ = أ^٢ + ب^٢

^٢١٣ = ^٢١٢ + ^٢٥

١٦٩ = ١٤٤ + ٢٥

١٦٩ = ١٦٩

٢٥، ٢٠، ١٥

ج^٢ = أ^٢ + ب^٢

^٢٢٥ = ^٢٢٠ + ^٢١٥

٦٢٥ = ٤٠٠ + ٢٢٥

٦٢٥ = ٦٢٥

٢٢) اكتب: فسر لماذا يمكنك استعمال طولي أي ضلعين في المثلث القائم الزاوية لإيجاد طول الضلع الثالث؟

لأنه تربط نظرية فيثاغورس أطوال الأضلاع الثلاثة حيث أن مربع طول الوتر يساوي مجموع مربعي طولي الساقين، فإذا علمت طولي ضلعين في مثلث قائم الزاوية أمكنك تعويض القيم في نظرية فيثاغورس لإيجاد طول الضلع المجهول.

٢٣) احسب محيط أ ب جـ.

أ) ٢٦م

ب) ٣٤م

جـ) ٦٠م

د) ٦٨م

أ ب = $\sqrt{\mathrm{٥٧٦} + \mathrm{١٠٠}}=\sqrt{\mathrm{٦٧٦}}$ = ٢٦م.

محيط المثلث = ٢٦ + ٢٤ + ١٠ = ٦٠م.

٢٤) إجابة قصيرة: وضع سلم طوله ١٠ أقدام على الحائط الرأسي لمنزل، بحيث تبعد حافة السلم السفلي ٦ أقدام من قاعدة المنزل.

على ارتفاع كم قدم من الحائط تصل حافة السلم العليا؟

الارتفاع = $\sqrt{\mathrm{١٠٠} - \mathrm{٣٦}}=\sqrt{\mathrm{٦٤}}$ = ٨ أقدام.