حلول الأسئلة
السؤال
(١٠، -٣)، (-٨، -٥)
الحل
م = () قانون نقطة المنتصف
م = (س١، ص١) = (١٠، -٣)، (س٢، ص٢) = (-٨، -٥)
م = ()
م = (١، -٤)
شاهد حلول جميع الاسئلة
حل أسئلة تدرب وحل المسائل
سم الزوج المرتب لكل نقطة مما يأتي:
١٩) ف
(٠,٥، -١)
٢٠) ك
(٠,٧٥، ٠,٥)
٢١) ر
(٠,٧٥، ١,٢٥)
٢٢) س
(١، -٠,٧٥)
٢٣) ت
(٠,٢٥، ٠,٧٥)
٢٤) ل
(-٠,٥، -٠,٥)
٢٥) ن
(-١,٢٥، -١,٢٥)
٢٦) ق
(-١، ٠,٢٥)
مثل كل نقطة مما يأتي وسمها:
٢٧) ()
٢٨) ()
٢٩) (-٣، )
٣٠) ()
٣١) (٤,٣، -٣,١)
٣٢) (-٣,٧٥، -٠,٥)
٣٣) (٠، ٢)، (٧، ٣)
م = () قانون نقطة المنتصف
م = (س١، ص١) = (٠، -٢)، (س٢، ص٢) = (٧، ٣)
م = ()
٣٤) (٥، -٢)، (٣، -٦)
م = () قانون نقطة المنتصف
م = (س١، ص١) = (٥، -٢)، (س٢، ص٢) = (٣، -٦)
م = ()
= (٤، -٤)
٣٥) (-٤، ٠)، (٠، ١٤)
م = () قانون نقطة المنتصف
م = (س١، ص١) = (-٤، ٠)، (س٢، ص٢) = (٠، ١٤)
م = ()
= (-٢، ٧)
٣٦) (١٠، -٣)، (-٨، -٥)
م = () قانون نقطة المنتصف
م = (س١، ص١) = (١٠، -٣)، (س٢، ص٢) = (-٨، -٥)
م = ()
م = (١، -٤)
٣٧) (-٥، ٥)، (٣، -٣)
م = () قانون نقطة المنتصف
م = (س١، ص١) = (-٥، ٥)، (س٢، ص٢) = (٣، -٣)
م = ()
م = (-١، ١)
٣٨) (-١٦، -٧)، (-٤، -٣)
م = () قانون نقطة المنتصف
م = (س١، ص١) = (-١٦، -٧)، (س٢، ص٢) = (-٤، -٣)
م = ()
م = (-١٠، -٥)
مثل كل زوج من الأزواج المرتبة الآتية، ثم أوجد المسافة بين النقطتين:
٣٩) (٤، ٥) (٢، ٢)
ج٢ = أ٢ + ب٢
حيث أ = ٢ - ٤ = -٢
ب = ٢ - ٥ = -٣
ج٢ = أ٢ + ب٢
ج = (-٢)٢ + (-٣)٢
ج = ٤ + ٩ = ١٣
ج =
ج = ٣,٦ وحدة تقريباً.
٤٠) (٦، ٢) (١، ٠)
ج٢ = أ٢ + ب٢
حيث أ = ١ - ٦ = -٥
ب = ٠ - ٢ = -٢
ج٢ = أ٢ + ب٢
ج = (-٥)٢ + (-٢)٢
ج = ٢٥ + ٤ = ٢٩
ج =
ج = ٥,٤ وحدة تقريباً.
٤١) (-٣، ٤) (١، ٣)
ج٢ = أ٢ + ب٢
حيث أ = ١ -(-٣) = ٤
ب = ٣ - ٤ = -١
ج٢ = أ٢ + ب٢
ج = (٤)٢ + (-١)٢
ج = ١٦ + ١ = ١٧
ج =
ج = ٤,١ وحدة تقريباً.
٤٢) (-٥، ١) (٢، ٤)
ج٢ = أ٢ + ب٢
حيث أ = ٢ -(-٥) = ٧
ب = ٤ - ١ = ٣
ج٢ = أ٢ + ب٢
ج = (٧)٢ + (٣)٢
ج = ٤٩ + ٩ = ٥٨
ج =
ج = ٧,٦ وحدة تقريباً.
٤٣) (٢,٥، -١) (-٣,٥، -٥)
ج٢ = أ٢ + ب٢
حيث أ = -٣,٥ -(٢,٥) = -٦
ب = -٥ - (-١) = -٤
ج٢ = أ٢ + ب٢
ج = (-٦)٢ + (-٤)٢
ج = ٣٦ + ١٦ = ٥٢
ج =
ج = ٧,٢ وحدة تقريباً.
٤٤) (٤، ٥) (-١، -٦,٣)
ج٢ = أ٢ + ب٢
حيث أ = -١ - ٤ = -٥
ب = -٦,٣ -(-٢,٣) = -٤
ج٢ = أ٢ + ب٢
ج = (-٥)٢ + (-٤)٢
ج = ٢٥ + ١٦ = ٤١
ج =
ج = ٦,٤ وحدة تقريباً.
٤٥) ملاحة: تنطلق عبارة من النقطة أ (٤، ١٢) الواقعة على الجزيرة كما في الشكل المجاور، وتتجه إلى المرفأ الواقع عند النقطة ب (٦، ٢) ما المسافة التي تقطعها العبارة إذا كانت كل وحدة على الخارطة تعادل ٠,٥ كلم؟
أ (٤، ١٢)، ب (٦، ٢)
ج٢ = أ٢ + ب٢
حيث أ = ٦ - ٤ = ٢
ب = ٢ - ١٢ = -١٠
ج٢ = ٢٢ + ٢١٠
ج٢ = ٤ + ١٠٠ = ١٠٤
ج =
ج = ١٠,٢ وحدة تقريباً.
المسافة التي تقطعها العبارة = ١٠,٢ × ٠,٥ = ٥,١ كم.
٤٦) جغرافيا: على الخارطة تقع الرياض في النقطة (٣، ٢,٥)، وتقع المنامة في النقطة (٦، ٤)، إذا كانت كل وحدة على الخارطة تمثل ١٢٥ كلم، فما المسافة الجوية التقريبية بين الرياض والمنامة؟
(٣، ٢,٥)، (٦، ٤)
ج٢ = أ٢ + ب٢
حيث أ = ٦ - ٣ = ٣
ب = ٤ - ٢,٥ = ١,٥
ج٢ = ٢٣ + ٢١,٥
ج٢ = ٩ + ٢,٢٥ = ١١,٢٥
ج =
ج = ٣,٤ وحدة تقريباً.
المسافة التقريبية بين الرياض والمنامة = ١٢٥ × ٣,٤ = ٤١٩ كلم.
أوجد مساحة الشكل في كل مما يأتي:
٤٧) .JPG)
ج٢ = أ٢ + ب٢
ج٢ = ٢٥ + ٢٩
ج٢ = ٢٥ + ٨١
ج٢ = ١٠٦
ج =
ج = ١٠,٣ وحدة تقريباً.
ج٢ = أ٢ + ب٢
ب٢ = ٢٢ + ٢٤
ب٢ = ٤ + ١٦
ب٢ = ٢٠
جـ =
جـ = ٤,٥ وحدة تقريباً.
مساحة المستطيل = الطول × العرض
= ١٠,٣ × ٤,٥
= ٤٦ وحدة مربعة تقريباً.
٤٨) .JPG)
ج٢ = أ٢ + ب٢
ج٢ = ٢٢ + ٢٣
ج٢ = ٢٤ + ٢٩
ج٢ = ١٣
ج =
ج = ٣,٦ وحدة تقريباً.
مساحة المربع = مربع طول الضلع
ج٢ = ١٣ وحدة مربعة.
أوجد إحداثيي نقطة المنتصف للقطعة المستقيمة الواصلة بين كل نقطتين فيما يأتي:
٤٩) (٤,٢٥، ٢,٥)، (٢,٥، -٣)
م = () قانون نقطة المنتصف
م =
م = ()
م = (٣,٣٧٥، -٠,٢٥)
٥٠) (٥، )، (-٣، )
م = () قانون نقطة المنتصف
م =
م = (، ١)
= (١، ١)
٥١) ()، ()
م = () قانون نقطة المنتصف
م =
م = ()
م = (-١٠، -٥)
٥٢) تحد: طبق ما تعلمته عن المسافة في المستوى الإحداثي لتحديد إحداثيات نقطتي نهاية قطعة مستقيمة ليست أفقية أو رأسية طولها ٥ وحدات.
(١، ٢)، (٤، ٦)
٥٣) اختر أداة: أرادت هيفاء إيجاد المسافة بين النقطتين أ (-٢,٤، ٣,٧)، ب (٤,٦، -١,٣)، أي الأدوات الآتية أكثر فائدة لها؟ برر إجابتك، ثم استعمل الأداة لحل المسألة.
أ (-٢,٤، ٣,٧)، ب (٤,٦، -١,٣)
الأداة: الآلة الحاسبة
ستكون مفيدة أكثر وعملية لإيجاد مربع والجذر التربيعي للأعداد التي بها كسوراً عشرية.
الحل: ٨,٦ وحدات.
٥٤) اكتب: استعمل كلماتك الخاصة في توضيح طريقة إيجاد طول قطعة مستقيمة غير رأسية أو أفقية نقطتا نهايتها (س١، ص١)، (س٢، ص٢).
ارسم على المستوى الإحداثي خطأ أفقياً من (س١، ص١) إلى (س٢، ص١).
ثم ارسم خطاً رأسياً من (س٢، ص٢) إلى (س٢، ص١) لتكون مثلثاً قائم الزاوية، حدد طولي الساقين الزاوية القائمة، ثم طبق نظرية فيثاغورس لتجد طول الوتر، وهو طول القطعة الأصلي.
٥٥) اكتب وضح كيف يرتبط قانون نقطة المنتصف، بإيجاد المتوسط الحسابي.
المتوسط الحسابي نجمع العددين ونقسمهما على ٢
قانون نقطة المنتصف نجمع الإحداثيين السينين ونقسم على ٢، ونجمع الإحداثيين الصاديين ونقسم على ٢ أي المتوسط الحسابي لكل من الإحداثيين السينين والصاديين
٥٦) تشير الخريطة أدناه إلى مواقع منازل الأصدقاء محمد، وخالد، ونواف، أوجد المسافة بين منزلي نواف وخالد؟
أ) ١٤ كلم.
ب) ٢٢ كلم.
جـ) ٢٦ كلم.
د) ٣٤ كلم.
المسافة بين منزلي نواف وخالد = = ٢٦ كلم.
٥٧) أوجد مساحة المستطيل أ ب جـ د الممثل على المستوى الإحداثي أدناه؟
أ) ٣٠ وحدة مربعة.
ب) ٥٠ وحدة مربعة.
جـ) ٦٠ وحدة مربعة.
د) ١٠٠ وحدة مربعة.
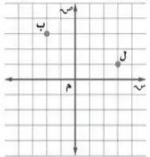
٥٩) إذا كانت (ل) تمثل منارة، و (ب) سفينة كما في التمثيل أدناه، ويوجد قارب صيد في منتصف المسافة بين ل و ب، فأي الإحداثيات الآتية تمثل موقع القارب؟
أ) (٢، )
ب) (١، )
جـ) (، ٢)
د) (، ٥)
م = () قانون نقطة المنتصف
م =
م = ()
م = (، ٢)
الإجابة الصحيحة ج

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)
.JPG)
.JPG)