استعمل الإنترنت أو أي مصدر آخر لتوضيح سبب تسمية المستوى الإحداثي في بعض الأحيان بالمستوى الديكارتي.

نسبة إلى العالم الفرنسي رينيه ديكارت صاحب فكرة الربط بين الهندسة والجبر وذلك بتمثيل النقطة في المستوى الإحداثي.

حل أسئلة تدرب وحل المسائل

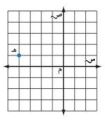
اكتب الزوج المرتب الذي يقابل كل نقطة من النقاط التالية، ثم حدد الربع الذي تقع فيه أو المحور الذي تقع عليه:

١١) أ

• أبدأ من نقطة الأصل.
• تحرك يساراً على محور السينات لتحدد الإحداثي السيني للنقطة أ وهو في هذه الحالة -٢.
• تحرك إلى الأعلى على محور الصادات لإيجاد الإحداثي الصادي وهو في هذه الحالة ٢.
• إذاً النقطة أ تقابل الزوج المرتب (-٢، ٢). وهي تقع في الربع الثاني.

١٢) ب

• أبدأ من نقطة الأصل.
• تحرك يميناً على محور السينات لتحدد الإحداثي السيني للنقطة ب وهو في هذه الحالة ٥.
• تحرك إلى الأعلى على محور الصادات لإيجاد الإحداثي الصادي وهو في هذه الحالة ٤.
• إذاً النقطة ب تقابل الزوج المرتب (٥، ٤). وهي تقع في الربع الأول.

١٣) د

• أبدأ من نقطة الأصل.
• تحرك يميناً على محور السينات لتحدد الإحداثي السيني للنقطة د وهو في هذه الحالة ٤.
• تحرك إلى الأسفل على محور الصادات لإيجاد الإحداثي الصادي وهو في هذه الحالة -٣.
• إذاً النقطة د تقابل الزوج المرتب (٤، -٣). وهي تقع في الربع الرابع.

١٤) ز

• أبدأ من نقطة الأصل.
• تحرك يساراً على محور السينات لتحدد الإحداثي السيني للنقطة ز وهو في هذه الحالة -٤.
• تحرك إلى الأسفل على محور الصادات لإيجاد الإحداثي الصادي وهو في هذه الحالة -١.
• إذاً النقطة ز تقابل الزوج المرتب (-٤، -١). وهي تقع في الربع الثالث.

١٥) ح

• أبدأ من نقطة الأصل وهو في هذه الحالة النقطة ح تقع عند ٠.
• تحرك إلى الأسفل على محور الصادات لإيجاد الإحداثي الصادي وهو في هذه الحالة -٤.
• إذاً النقطة ح تقابل الزوج المرتب (٠، -٤). وهي تقع على محور الصادات.

١٦) ل

• أبدأ من نقطة الأصل.
• تحرك يميناً على محور السينات لتحدد الإحداثي السيني للنقطة ل وهو في هذه الحالة ١.
• تقع النقطة على المحور أي الإحداثي السيني في هذه الحالة ٠.
• إذاً النقطة ل تقابل الزوج المرتب (١، ٠). وهي تقع في محور السينات.

ارسم المستوى الإحداثي في ورقة رسم بياني، ثم مثل كلاً من النقاط الآتية عليه، وسمها:

١٧) ك (٥، ٦)

١٨) ن (-٢، ١)

١٩) س (٧، -٨)

٢٠) ص (٣، ٠)

٢١) ر (-١، -٧)

٢٢) ط (٠، ٦)

٢٣) خ (-٤، ٠)

٢٤) ي (٠، -٥)

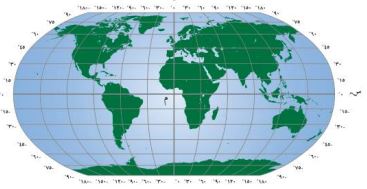
جغرافيا: يمكن تقسيم خريطة العالم بحسب المستوى الإحداثي، حيث (س، ص) يمثلان (درجات الطول، درجات العرض)، استعمل خريطة العالم لحل السؤالين ٢٥، ٢٦:

٢٥) في أي قارة تقع النقطة (٣٠°طول، -١٥°عرض)؟

قارة إفريقيا.

٢٦) أي القارات تقع كاملة في الربع الأول؟

قارة آسيا.

٢٧) هندسة: مثل بيانياً أربع نقاط على المستوى الإحداثي بحيث تشكل رؤوس مربع عند وصلها معاً، ثم حدد الأزواج المرتبة المقابلة لها.

٢٨) بحث: استعمل الإنترنت أو أي مصدر آخر لتوضيح سبب تسمية المستوى الإحداثي في بعض الأحيان بالمستوى الديكارتي.

نسبة إلى العالم الفرنسي رينيه ديكارت صاحب فكرة الربط بين الهندسة والجبر وذلك بتمثيل النقطة في المستوى الإحداثي.

حدد ما إذا كانت كل عبارة مما يأتي صحيحة دائماً أم صحيحة أحياناً أم غير صحيحة أبداً، وضح إجابتك بإعطاء مثال مضاد:

٢٩) كل من الإحداثيين السيني والصادي لنقطة تقع في الربع الثالث سالب.

صحيحة دائماً، كلا الإحداثيين سالب.

٣٠) الإحداثي الصادي لنقطة تقع على محور الصادات سالب.

صحيحة أحياناً، أحياناً سالبة إذا وقعت في أسفل المحور، أحياناً موجبة إذا وقعت في أعلى المحور، النقطتان (٠، -٢)، (٢، ٠) كلتاهما تقع على محور الصادات.

٣١) الإحداثي الصادي لنقطة تقع في الربع الثاني سالب.

غير صحيحة أبداً، الإحداثي الصادي في الربع الثاني دائماً موجب.

٣٢) مسألة مفتوحة: اقترح طريقة تحدد من خلالها الربع الذي تقع فيه نقطة ما دون الاستعانة بالتمثيل البياني، ثم أعط مثالاً يوضح ذلك.

باستخدام طريقة الإشارات.

مثال: (٢، -٣)

٢ تقع في المحور السيني و-٣ تقع في المحور الصادي أي تقع في الربع الثالث.

٣٣) اكتب وضح لماذا يختلف موقع النقطة أ (١، -٢) عن موقع النقطة ب (-٢، ١).

تبعد النقطة أ وحدة واحدة إلى اليمين ووحدتين إلى الأسفل من نقطة الأصل (الربع الرابع) وتبعد النقطة ب وحدتين إلى اليسار ووحدة واحدة إلى الأعلى من نقطة الأصل (الربع الثاني).

٣٤) أي النقاط التالية تقع داخل المثلث المرسوم في الشكل أدناه؟

أ) (-١، ٢)

ب) (-٤، -١)

جـ) (١، ٣)

د) (٢، -٢)

٣٥) ما إحداثيات النقطة هـ في الشكل أدناه؟

أ) (٤، -١)

ب) (-٤، ١)

جـ) (١، ٤)

د) (١، -٤)