حل أسئلة تدرب وحل المسائل

أوجد المسافة بين كل نقطتين فيما يأتي:

٩) (٥، ٨)، (٥، ٧)

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٥} -\mathrm{٥})}^{\mathrm{٢}} + {(\mathrm{٧} - \mathrm{٨})}^{\mathrm{٢}}}$

ف = $\sqrt{{\left(\mathrm{٠}\right)}^{\mathrm{٢}} + {\left(\mathrm{١}\right)}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{١}}$

ف = ١

١٠) (٦، -٩)، (٩، -٩)

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٩} -\mathrm{٦})}^{\mathrm{٢}} + {(-\mathrm{٩} + \mathrm{٩})}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{٩} + \mathrm{٠}}$

ف = ٣

١١) (٣، -٣)، (٧، ٢)

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٧} -\mathrm{٣})}^{\mathrm{٢}} + {(-\mathrm{٣} - \mathrm{٢})}^{\mathrm{٢}}}$

ف = $\sqrt{{\left(\mathrm{٤}\right)}^{\mathrm{٢}} + {(-\mathrm{٥})}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{١٦} + \mathrm{٢٥}}$

ف = $\sqrt{\mathrm{٤٢}}$

١٢) (-٧، ٨)، (٣، ١٠)

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٣}+\mathrm{٧})}^{\mathrm{٢}} + {(\mathrm{١٠} - \mathrm{٨})}^{\mathrm{٢}}}$

ف = $\sqrt{{\left(\mathrm{١٠}\right)}^{\mathrm{٢}} + {\left(\mathrm{٢}\right)}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{١٠٠} + \mathrm{٤}}$

ف = $\sqrt{\mathrm{١٠٤}} = \mathrm{٢}\sqrt{\mathrm{٢٦}}$

١٣) (-١١، ٩)، (٣، -٤)

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٣} +\mathrm{١١})}^{\mathrm{٢}} + {(-\mathrm{٤} - \mathrm{٩})}^{\mathrm{٢}}}$

ف = $\sqrt{{\left(\mathrm{٠}\right)}^{\mathrm{٢}} + {\left(\mathrm{١}\right)}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{١}}$

ف = ١

١٤) (-٣، ٥)، (٥، -٣)

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٥} +\mathrm{٣})}^{\mathrm{٢}} + {(-\mathrm{٣} - \mathrm{٥})}^{\mathrm{٢}}}$

ف = $\sqrt{{\left(\mathrm{٨}\right)}^{\mathrm{٢}} + {(-\mathrm{٨})}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{٦٤} + \mathrm{٦٤}}$

ف = $\sqrt{\mathrm{١٢٨}}\approx \mathrm{٨}\sqrt{\mathrm{٢}}$

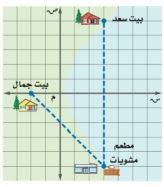
١٥) تحديد مواقع: أراد سعد وجمال أن يلتقيا في مطعم مشويات كما في التمثيل المجاور فاستعمل سعد قاربه للوصول إلى المطعم، في حين استعمل جمال سيارته، علماً بأن طول ضلع كل مربع من المستوى الإحداثي يمثل كيلو متراً واحداً.

أ) ما المسافة التي قطعها؟

(٣، ٥)، (٣، -٥)

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٣} -\mathrm{٣})}^{\mathrm{٢}} + {(-\mathrm{٥} - \mathrm{٥})}^{\mathrm{٢}}}$

ف = $\sqrt{ \mathrm{١٠٠} }$

ف = ١٠

إذن المسافة التي يقطعها سعد = ١٠ كلم.

ب) ما المسافة التي قطعها جمال؟

(٣، ٥)، (-٢، ٠)

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(-\mathrm{٢}-\mathrm{٣})}^{\mathrm{٢}} + {(\mathrm{٠} - \mathrm{٥})}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{٥٠}}$

٥$\sqrt{\mathrm{٢}}$ = ٧,٠٧

كلم تقريباً إذن المسافة التي يقطعها سعد = ٥$\sqrt{\mathrm{٢}}$ = ٧,٠٧ كلم تقريباً.

جـ) ما النسبة بين المسافة التي قطعها سعد إلى المسافة التي قطعها جمال؟

النسبة بين سعد وجمال = ١٠٠: $\sqrt{\mathrm{٥٠}}$

$\frac{\mathrm{١٠}}{\sqrt{\mathrm{٥٠}}}\times \frac{\sqrt{\mathrm{٥٠}}}{\sqrt{\mathrm{٥٠}}}$ = $\frac{\mathrm{١٠}\sqrt{\mathrm{٥٠}}}{\mathrm{٥٠}}$

= $\frac{\sqrt{\mathrm{٥٠}}}{\mathrm{٥}}$

= $\frac{\sqrt{\mathrm{٥}\times \mathrm{٢}\times \mathrm{٥}}}{\mathrm{٥}}=\frac{\mathrm{٥}\sqrt{\mathrm{٢}}}{\mathrm{٥٠}}$

= $\sqrt{\mathrm{٢}}$ = ١,٤١ تقريباً.

في الأسئلة ١٦ - ١٩ أوجد القيم الممكنة للمتغير (أ)، مستعملاً إحداثيات كل نقطتين، والمسافة المعطاة بينهما:

١٦) (-٩، -٢)، (أ، ٥)؛ ف = ٧

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

٧٧ = $\sqrt{{(أ+\mathrm{٩})}^{\mathrm{٢}} + {(\mathrm{٥} + \mathrm{٢})}^{\mathrm{٢}}}$

٧٧ = $\sqrt{{أ}^{\mathrm{٢}} + \mathrm{٨١} + \mathrm{١٨}أ + {\left(\mathrm{٧}\right)}^{\mathrm{٢}}}$

٧٧ = $\sqrt{{أ}^{\mathrm{٢}} + \mathrm{٨١} + \mathrm{١٨}أ + \mathrm{٤٩}}$

٧٧ = $\sqrt{{أ}^{\mathrm{٢}} + \mathrm{١٨}أ + \mathrm{١٣٠}}$

٤٩ = أ^٢ + ١٣٠ + ١٨أ

أ + ١٨أ + ٨١ = ٠

(أ + ٩) (أ + ٩) = ٠

أ = -٩

١٧) (أ، -٦)، (-٥، ٢)؛ ف = ١٠

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

١٠ = $\sqrt{{(-\mathrm{٥}-أ)}^{\mathrm{٢}} + {(\mathrm{٢} + \mathrm{٦})}^{\mathrm{٢}}}$

١٠ = $\sqrt{{أ}^{\mathrm{٢}} + \mathrm{٢٥} + \mathrm{١٠}أ + \mathrm{٦٤}}$

١٠٠ = أ^٢ + ١٠أ + ٨٩

أ^٢ + ١٠أ - ١١ = ٠

(أ + ١١) (أ - ١) = ٠

أ = -١١

‌أ = ١

١٨) (أ، ٠)، (٣، ١)؛ ف = $\sqrt{\mathrm{٢}}$

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

٢ = $\sqrt{{(\mathrm{٣} - أ)}^{\mathrm{٢}} + {(\mathrm{٠} -\mathrm{١})}^{\mathrm{٢}}}$

٢ = $\sqrt{{أ}^{\mathrm{٢}} + \mathrm{٩} -\mathrm{٦}أ + \mathrm{١}}$

٢ = أ^٢ - ٦أ + ١٠

أ^٢ - ٦أ + ٨ = ٠

(أ - ٢) (أ - ٤) = ٠

أ = ٢

أ = ٤

١٩) (٤، أ)، (٨، ٤)؛ ف = ٢$\sqrt{\mathrm{٥}}$

ف = $\sqrt{{({س}_{\mathrm{٢}} - {س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

٢$\sqrt{\mathrm{٥}}$ = $\sqrt{{(\mathrm{٨} - \mathrm{٤})}^{\mathrm{٢}} + {(\mathrm{٤} -أ)}^{\mathrm{٢}}}$

٢٠ = أ + ١٦ - ٨أ + ١٦

٢٠ - ٣٢ = أ - ٨أ

أ - ٨أ + ١٢ = ٠

(أ - ٢) (أ - ٦) = ٠

أ = ٢

أ = ٦

أوجد المسافة بين كل نقطتين فيما يأتي:

٢٠) (٤، ٢)، (٦، $-\frac{\mathrm{٢}}{\mathrm{٣}}$)

ف = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} {({ص}_{\mathrm{٢}} -{ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٦} - \mathrm{٤})}^{\mathrm{٢}} + {(\frac{-\mathrm{٢}}{\mathrm{٣}}-\mathrm{٢})}^{\mathrm{٢}}}$

ف = $\sqrt{{\left(\mathrm{٢}\right)}^{\mathrm{٢}} + {\left(\frac{-\mathrm{٢} -\mathrm{٦}}{\mathrm{٢}}\right)}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{٤} + {\left(\frac{-\mathrm{٨}}{\mathrm{٣}}\right)}^{\mathrm{٢}}}=\sqrt{\mathrm{٤} +\frac{\mathrm{٦٤}}{\mathrm{٩}}}$

ف = $\sqrt{\frac{\mathrm{٣٦} + \mathrm{٦٤}}{\mathrm{٩}}}=\sqrt{\frac{\mathrm{١٠٠}}{\mathrm{٩}}}$

ف = $\frac{\mathrm{١٠}}{\mathrm{٣}}=\frac{\mathrm{١}}{\mathrm{٣}}$٣

٢١) ($\frac{\mathrm{٤}}{\mathrm{٥}}، -\mathrm{١}$)، (٢، -$\frac{\mathrm{١}}{\mathrm{٢}}$)

ف = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} {({ص}_{\mathrm{٢}} -{ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٢} - \frac{\mathrm{٤}}{\mathrm{٥}})}^{\mathrm{٢}} + {(-\mathrm{١}+\frac{\mathrm{١}}{\mathrm{٢}})}^{\mathrm{٢}}}$

ف = $\sqrt{{\left(\frac{\mathrm{١٠} -\mathrm{٤}}{\mathrm{٥}}\right)}^{\mathrm{٢}} + {\left(\frac{-\mathrm{١}}{\mathrm{٢}}\right)}^{\mathrm{٢}}}$

ف = $\sqrt{{\left(\frac{\mathrm{٦}}{\mathrm{٥}}\right)}^{\mathrm{٢}} + {\left(\frac{-\mathrm{١}}{\mathrm{٢}}\right)}^{\mathrm{٢}}}$

ف = $\sqrt{\frac{\mathrm{٣٦}}{\mathrm{٢٥}}+\frac{\mathrm{١}}{\mathrm{٤}}}$

ف = $\sqrt{\frac{\mathrm{١٤٤} + \mathrm{٢٥}}{\mathrm{١٠٠}}}$

ف = $\sqrt{\frac{\mathrm{١٦٩}}{\mathrm{١٠٠}}}$

ف = $\frac{\mathrm{١٣}}{\mathrm{١٠}}=\frac{\mathrm{٣}}{\mathrm{١٠}}$١

٢٢) (٤$\sqrt{\mathrm{٥}}، \mathrm{٧}$)، (٦$\sqrt{\mathrm{٥}}، \mathrm{١}$)

ف = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} {({ص}_{\mathrm{٢}} -{ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٦}\sqrt{\mathrm{٥}} - \mathrm{٤}\sqrt{\mathrm{٥}})}^{\mathrm{٢}} + {(\mathrm{١}-\mathrm{٧})}^{\mathrm{٢}}}$

ف = $\sqrt{{\left(\mathrm{٢}\sqrt{\mathrm{٥}}\right)}^{\mathrm{٢}} + {(-\mathrm{٦})}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{٢٠} + \mathrm{٣٦}}$

ف = $\sqrt{\mathrm{٥٦}}$

ف = ٢$\sqrt{\mathrm{١٤}}$

٢٣) هندسة: أوجد محيط الشكل الرباعي أ ب جـ د الذي رؤوسه أ (-٣، -٤)، ب (٤، ٥)، د (٦، -٥) ثم قرب الناتج إلى أقرب جزء من عشرة.

ف_(أب) = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} {({ص}_{\mathrm{٢}} -{ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف_(أب) = $\sqrt{{(-\mathrm{١} - (-\mathrm{٣}\left)\right)}^{\mathrm{٢}} + {(\mathrm{٤}+\mathrm{٤})}^{\mathrm{٢}}}$

ف_(أب) = $\sqrt{{\left(\mathrm{٢}\right)}^{\mathrm{٢}} + {\left(\mathrm{٨}\right)}^{\mathrm{٢}}}$

ف_(أب) = $\sqrt{\mathrm{٤} + \mathrm{٦٤}}$

ف_(أب) = $\sqrt{\mathrm{٦٨}}$

ف_{(جـ ب)} = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} {({ص}_{\mathrm{٢}} -{ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف_{(جـ ب)} = $\sqrt{{(\mathrm{٤} +\mathrm{١})}^{\mathrm{٢}} + {(\mathrm{٥}-\mathrm{٤})}^{\mathrm{٢}}}$

ف_{(جـ ب)} = $\sqrt{\mathrm{٢٥} + \mathrm{١}}$

ف_{(جـ ب)} = $\sqrt{\mathrm{٢٦}}$

ف_{(جـ د)} = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} {({ص}_{\mathrm{٢}} -{ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف_{(جـ د)} = $\sqrt{{(\mathrm{٦} - \mathrm{٤})}^{\mathrm{٢}} + {(-\mathrm{٥}-\mathrm{٥})}^{\mathrm{٢}}}$

ف_{(جـ د)} = $\sqrt{{\left(\mathrm{٢}\right)}^{\mathrm{٢}} + {(-\mathrm{١٠})}^{\mathrm{٢}}}$

ف_{(جـ د)} = $\sqrt{\mathrm{٤} + \mathrm{١٠٠}}$

ف_{(جـ د)} = $\sqrt{\mathrm{١٠٤}}$

ف_(أد) = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} {({ص}_{\mathrm{٢}} -{ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف_(أد) = $\sqrt{{(\mathrm{٦} +\mathrm{٣})}^{\mathrm{٢}} + {(-\mathrm{٥}+\mathrm{٤})}^{\mathrm{٢}}}$

ف_(أد) = $\sqrt{{\left(\mathrm{٩}\right)}^{\mathrm{٢}} + {(-\mathrm{١})}^{\mathrm{٢}}}$

ف_(أد) = $\sqrt{\mathrm{٨٢}}$

محيط الشكل الرباعي = $\sqrt{\mathrm{٨٢}}$ + $\sqrt{\mathrm{١٠٤}}$ + $\sqrt{\mathrm{٢٦}}$ + $\sqrt{\mathrm{٦٨}}$ = ٣٢,٦ وحدات.

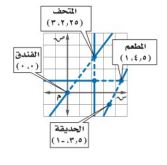
٢٤) سياحة: يستعمل أحمد نظام تحديد المواقع العالمي (GPS) كما في التمثيل المجاور للانتقال من الفندق إلى المتحف الوطني وإلى المطعم ثم إلى الحديقة العامة، ويمثل طول ضلع كل مربع من المستوى الإحداثي ٥٠٠م، قرب إجابتك إلى أقرب جزء من مئة.

أ) ما المسافة التي يقطعها من الفندق إلى المتحف؟

ف = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} {({ص}_{\mathrm{٢}} -{ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٠}- \mathrm{٢٥}.\mathrm{٢})}^{\mathrm{٢}} + {(\mathrm{٠}-\mathrm{٣})}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{٠٦٢٤}.\mathrm{١٤}}$ = ٣,٧٥ × ٥٠٠

ف = ١٨٧٥ م.

ب) ما المسافة بين المتحف والمطعم؟

ف = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} {({ص}_{\mathrm{٢}} -{ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٥}.\mathrm{٤} - \mathrm{٢٥}.\mathrm{٢})}^{\mathrm{٢}} + {(\mathrm{١}-\mathrm{٣})}^{\mathrm{٢}}}$

ف = $\sqrt{{\left(\mathrm{٢}\sqrt{\mathrm{٥}}\right)}^{\mathrm{٢}} + {(-\mathrm{٦})}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{٠٦٢٥}.\mathrm{٥} + \mathrm{٤}}$

ف = ٣,٠١٠٣٩ × ٥٠٠

ف = ١٥٠٥,٢٠ م.

جـ) أوجد المسافة المباشرة من الحديقة العامة إلى الفندق.

ف = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} {({ص}_{\mathrm{٢}} -{ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(\mathrm{٠}- \mathrm{٥}.\mathrm{٣})}^{\mathrm{٢}} + {(\mathrm{٠}+\mathrm{١})}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{٢٥}.\mathrm{١٢} + \mathrm{١}}$

ف = ٣,٦٤ × ٥٠٠

ف = ١٨٢٠,٠٣ م.

٢٥) تحد: إذا كانت أ (-٧، ٣)، ب (٤، ٠)، جـ (-٤، ٤) إحداثيات رؤوس مثلث، فناقش طريقتين مختلفتين لتحديد ما إذا كان المثلث أ ب جـ قائم أم لا.

إحدى الطرق هي إيجاد الميل لكل معكوس سالب ميل الآخر فإن المثلث قائم الزاوية، أما الطريقة الأخرى فهي إيجاد المسافة بين كل زوج من النقاط ثم تتحقق من إمكانية تطبيق معكوس نظرية فيثاغورس.

٢٦) تبرير: فسر لماذا تكون هناك قيمتان ممكنتان عند البحث عن الإحداثي المجهول لنقطة عند إعطاء إحداثيات نقطتين والمسافة بينهما.

يتطلب قانون المسافة بين نقطتين تربيع القيم وعند تعويض الإحداثيات والمتغير أ في القانون وتبسيطه فإن النتيجة تكون معادلة تربيعية ينتج عن حلها قيمتان ممكنتان للمتغير أ.

٢٧) إجابة قصيرة: انطلق قاربان من الموقع نفسه وفي الوقت نفسه كما في التمثيل أدناه، فاتجه أحدهما شرقاً ثم شمالاً، أما الآخر فاتجه جنوباً ثم غرباً، ما المسافة بينهما؟

(٣، ٤)، (-٦، -٨)

ف = $\sqrt{{({س}_{\mathrm{٢}} -{س}_{\mathrm{١}})}^{\mathrm{٢}} + {({ص}_{\mathrm{٢}} - {ص}_{\mathrm{١}})}^{\mathrm{٢}}}$

ف = $\sqrt{{(-\mathrm{٦} -\mathrm{٣})}^{\mathrm{٢}} + {(-\mathrm{٨} -\mathrm{٤})}^{\mathrm{٢}}}$

ف = $\sqrt{\mathrm{٨١} + \mathrm{١٤٤}}= \sqrt{\mathrm{٢٢٥}}$

ف = ١٥ المسافة بينهما.