للوصول السريع إلى الدروس والاختبارات..
حمل تطبيق سبورة من متجر جوجل

حل أسئلة تدرب وحل المسائل
احسب قيمة كل عبارة فيما يأتي إذا كانت أ = -٢، ب = -٣، جـ = ٢، س = ٢,١، ص = ٣، ع = ٤,٢:
١٠) ٤أ -
٤أ -
= ٤ × - ٢ -
= - ٨ -
= - ٨ - ٥
= - ١٣
١١) -
-
= -
= -
= - ٨ + ٦,٠
= - ٧,٤
١٢) - ٣
- ٣
= - ٣
= - ٣
= ١١,٤ - ٣
= ٨,٤
١٣) ٣ - ٣
٣ - ٣
= ٣ - ٣
= ٣ × ٢٥ - ٣
= ٧٢
١٤) + ٦ب
+ ٦ع
= + ٦ × - ٣
= ٨,٤ - ١٨
= - ٩,٦
١٥) - ٤
- ٤
= - ٤
= - ٤ × ١ + ٢ × ٢,٢
= - ٤ + ٤,٤
= ٠,٤
حل كلاً من المعادلات الآتية، ومثل مجموعة الحل بيانياً:
١٦) = ٥
= ٥
ن - ٣ = ٥ أو ن - ٣ = - ٥
ن - ٣ + ٣ = ٥ + ٣
ن = - ٢، ن = ٨
١٧) = ١
= ١
ف + ١٠ = ١ أو ف + = - ١
ف + ١٠ - ١٠ = ١ - ١٠ أو ف + ١٠ - ١٠ = - ١ - ١٠
ف = - ٩ أو ف = - ١١
١٨) = -٥
لا يوجد مسافات بالسالب مجموعة الحل:
١٩) = ٢٠
= ٢٠
٤ق - ٨ = ٢٠ أو ٤ق - ٨ = - ٢٠
٤ق - ٨ + ٨ = ٢٠ + ٨ أو ٤ق - ٨ + ٨ = - ٢٠ + ٨
٤ق = ٢٨ أو ٤ق = - ١٢
ق = ٧ أو ق = - ٧
٢٠) = -٣
لا يوجد مسافات بالسالب مجموعة الحل:
٢١) = ٦
-٢ص + ٦ = ٦ أو -٢ص + ٦ = - ٦
-٢ص + ٦ - ٦ = ٦ - ٦ أو -٢ص + ٦ - ٦ = - ٦ - ٦
- ٢ص = ٠ أو - ٢ص = -١٢
ص = ٠ أو ص = ٦
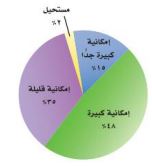
٢٢) دراسة مسحية: يبين التمثيل بالقطاعات الدائرية المجاور نتائج دراسة مسحية وجه فيها السؤال الآتي إلى عدد من الشباب: "ما إمكانية أن تصبح ثرياً يوماً ما؟" فإذا كانت نسبة الخطأ في هذا المسح ٤٪، فما مدى النسبة المئوية للشباب الذين أجابوا بأن إمكانية أن يصبحوا أثرياء كبيرة جداً؟
= ٤
س - ١٥ = ٤ أو س - ١٥ = - ٤
س - ١٥ + ١٥ = ٤ + ١٥ أو س - ١٥ + ١٥ = - ٤ + ١٥
س = ١٩ أو س = ١١
مدى النسبة المئوية للشباب ما بين ١١٪ إلى ١٩٪
٢٣) حوار: يعطى المتكلم في برنامج حواري متلفز فرصة الحديث لمدة دقيقتين مع فارق ٥ ثوان.
أ) أوجد أطول وأقصر مدة ممكنة للحديث بالدقائق وبالثواني.
- أطول مدة ممكنة دقيقتان و٥ ثواني.
- أقصر مدة ممكنة دقيقة و٥٥ ثانية.
ب) أوجد أطول وأقصر مدة ممكنة للحديث بالثواني.
- أطول مدة ممكنة = (٢ × ٦٠) + ٥ = ١٢٥ ثانية.
- أقصر مدة ممكنة = ٦٠ + ٥٥ = ١١٥ ثانية.
اكتب معادلة تتضمن القيمة المطلقة لكل من التمثيلين الآتيين:
٢٤) .JPG)
نقطة المنتصف بين - ٦ و٦ هي ٠ تبعد ٦ وحدات عن -٦ و٦ وحدات عن ٦
= ٦
٢٥) .JPG)
نقطة المنتصف بين ٢ و -٦ هي -٢ تبعد ٤ وحدات عن ٢ و٤ وحدات عن -٦
= ٤
حل كلاً من المعادلات الآتية، ومثل مجموعة الحل بيانياً:
٢٦) = ١٠
- ب - ٢ = ١٠ اضرب كلا الطرفين في - ٢ - ب - ٢ = - ١٠
ب + ٤ = -٢٠ اطرح ٤ من كلا الطرفين ب + ٤ = ٢٠
ب = - ٢٤ أو ب = ١٦
٢٧) = ١٢
- ٣د + ٦ = ١٢ اطرح ٦ من كلا الطرفين - ٣د + ٦ = - ١٢
- ٣د = ٦ اقسم كلا الطرفين على - ٣ - ٣د = - ١٨
د = - ٢ أو د = ٦
٢٨) ٤ - ٣ = ١٠
- ٣ = ٦
= - ٢
مجموعة الحل:
٢٩) = ١٢
٥ف - ٣ = ١٢ أو ٥ف - ٣ = - ١٢
٥ف - ٣ + ٣ = ١٢ + ٣ أو ٥ف - ٣ + ٣ = ١٢ + ٣
٥ف = ١٥ أو ٥ف = - ٩
ف = ٣ أو ف =
مجموعة الحل: {، ٣}
٣٠) مضمار: مضمار سباق التتابع ٤ × ٤٠٠ هو سباق يتناوب فيه ٤ عدائين الجري مسافة ٤٠٠ متر أو دورة واحدة لكل منهم حول المضمار.
أ) إذا أنهى العداء الأول دورته في ٥٢ ثانية أو ناقص ٢ ثانية، فاكتب معادلة لإيجاد أسرع وأبطأ زمن له.
= ٢
س - ٥٢ = ٢ أو س - ٥٢ = -٢
س - ٥٢ + ٥٢ = ٢ + ٥٢ أو س - ٥٢ + ٥٢ = - ٢ + ٥٢
س = ٥٤ أو س = ٥٠
مجموعة الحل: {٥٠، ٥٤}
ب) إذا أنهى العداء الثاني دورته في ٥٣ ثانية زائد أو ناقص ثانية واحدة، فاكتب معادلة لإيجاد أسرع وأبطأ زمن له.
= ١
س - ٥٣ = ١ أو س - ٥٣ = -١
س - ٥٣ + ٥٣ = ١ + ٥٣ أو س - ٥٣ + ٥٣ = - ١ + ٥٣
س = ٥٤ أو س = ٥٢
مجموعة الحل: {٥٢، ٥٤}
٣١) سيارات: تتأثر دقة مقياس سرعة السيارة بعدة عوامل؛ منها قطر الإطارات، فإذا كان الفارق عن القراء الدقيقة عند السرعة ٥٠ كلم/س هو ٣ كلم/س.
أ) فما مدى السرعة الحقيقية عندما تكون السرعة ٥٠ كلم/س؟
= ٣
س - ٥٠ = ٣ أو س - ٥٠ = -٣
س - ٥٠ + ٥٠ = ١ + ٥٠ أو س - ٥٠ + ٥٠ = - ١ + ٥٠
س = ٥٣ أو س = ٤٧
مدى السرعة ما بين ٤٧ و٥٣ كيلو متر/ ساعة.
ب) إذا علمت أنه تكون السرعة ٤٥ كلم/س يصبح فارق السرعة ١ كلم/س فقط، فماذا تستنتج؟
كلما قلت السرعة زادت الدقة.
اكتب معادلة تتضمن قيمة مطلقة لكل من التمثيلات الآتية:
٣٢) .JPG)
= ٤
٣٣) .JPG)
=
٣٤) .JPG)
= ١
٣٥) صوتيات: يوجد في أحد المدرجات حوالي ٢٠٠٠٠ شخص بفارق لا يجاوز ألف شخص أكثر أو أقل، يمكنهم سماع الأصوات الطبيعية بوضوح.
أ) اكتب معادلة تتضمن القيمة المطلقة لتمثل الحد الأقصى لعدد الأشخاص الذين يمكنهم سماع الأصوات الطبيعية في هذا المدرج بوضوح (افترض أن ن = عدد الأشخاص الذين يمكنهم سماع الأصوات بوضوح).
= ١٠٠٠
ب) ما مدى عدد الأشخاص في الفقرة أ؟
= ١٠٠٠
ن - ٢٠٠٠٠ = ١٠٠٠ أو ن - ٢٠٠٠٠ = - ١٠٠٠
ن = ٢١٠٠٠ أو ن = ١٩٠٠٠
مدى عدد الأشخاص من ١٩٠٠٠ إلى ٢١٠٠٠,
٣٦) قراءة: اتفق طلاب الثالث المتوسط في مدرسة على قراءة فصل من كتاب ينتهي عند الصفحة ٢٠٣، مع زيادة أو نقص عشر صفحات.
أ) اكتب معادلة القيمة المطلقة التي تمثل أرقام الصفحات التي يمكن أن يتوقف عندها الطلاب عن القراءة.
= ١٠
ب) اكتب مدى الصفحات التي يمكن أن يتوقف عندها الطلاب عن القراءة.
= ١٠
س - ٢٠٣ = ١٠ أو س - ٢٠٣ = -١٠
س - ٢٠٣ + ٢٠٣ = ١٠ + ٢٠٣ أو س - ٢٠٣ + ٢٠٣= ١٠ + ٢٠٣
س = ٢١٣ أو س = ١٩٣
مدى عدد الصفحات من ٩١٣ إلى ٢١٣ صفحة.
٣٧) مسألة مفتوحة: صف موقفاً من واقع الحياة يمكن تمثيله بالمعادلة: = ١٠.
اشترك طلاب الصف الخامس في مسابقة الأدب كان منهم أربع طلاب يشاركون بالقصة والباقي ١٠ طلاب يشاركون بالشعر.
فما مدى عدد الطلاب المشاركين في المسابقة؟
٣٨) تبرير: مفترضاً أن جـ عدد صحيح، حدد ما إذا كانت كل من العبارات الآتية صحيحة أحياناً أو صحيحة دائماً أو غير صحيحة أبداً، وفسر تبريرك:
أ) قيمة أكبر من الصفر.
أحياناً عندما س = -١، القيمة = ٠
ب) حل المعادلة: = ٠ عدد أكبر من الصفر.
أحياناً عندما جـ < ٠
جـ) ليس للمتباينة: + جـ < ٠ حلاً.
أحياناً عندما جـ < ٠ فالمتباينة صحيحة.
٣٩) تبرير: لماذا لا يمكن أن تكون القيمة المطلقة سالبة؟
القيمة المطلقة تمثل البعد عن الصفر على خط الأعداد والبعد لا يمكن أن يكون بالسالب.
٤٠) اكتشف الخطأ: حل كل من علي وعبد الرحمن المعادلة: = -٣ كما هو موضح أدناه، فأيهما إجابته صحيحة؟ ولماذا؟
عبد الرحمن؛ لأن القيمة المطلقة لا يمكن أن تكون سالبة.
٤١) اكتب: وضح لماذا يمكن أن يكون لمعادلة القيمة المطلقة حلان أو حل واحد أو لا يكون لها حل، وأعط مثالاً كل حالة.
- يكون للمعادلة حلان عندما تكون القيمة المطلقة تساوي عدداً موجباً.
- وحل وحيد إذا كانت القيمة المطلقة تساوي صفر.
- وليس لها حل إذا كانت القيمة المطلقة سالبة.
وتمثل القيمة المطلقة أبعاداً والبعد لا يكون سالب
- معادلة لها حلان = ٢
- معادلة لها حل واحد = ٠
- معادلة ليس لها حل = - ١
٤٢) هندسة: ما محيط الدائرة التي مساحتها ٢٥ ط سنتمتراً مربعاً؟
أ) ٥ ط سم
ب) ١٠ ط سم
جـ) ٥٠ ط سم
د) ٦٢٥ ط سم
مساحة الدائرة = ط نق٢ = ٢٥ط
نق = = ٥
محيط الدائرة = ٢ط نق = ٢ × ط نق = ٢ × ٥ ط
= ١٠ ط
٤٣) أي المعادلات التالية تمثل الخطوة الثانية في عملية الحل الموضحة؟
الخطوة ١: ٤(٢س + ٧) - ٦ = ٣س
الخطوة ٢: ـــــــــــــــ
الخطوة ٣: ٥س + ٢٨ - ٦ = ٠
الخطوة ٤: ٥س = - ٢٢
الخطوة ٥: س = - ٤,٤
أ) ٤(٢س - ٦) + ٧ = ٣س
ب) ٤(٢س + ١) = ٣س
جـ) ٨س + ٧ - ٦ = ٣س
د) ٨س + ٢٨ -٦ = ٣س
للوصول السريع إلى الدروس والاختبارات..
حمل تطبيق سبورة من متجر جوجل



.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)


النقاشات