حلول الأسئلة
السؤال
أوجد (ق. م. أ) لكل مجموعة وحيدات حد مما يأتي:
الحل
١٢ك ر، ٨ر ٢ ، ١٦ر ن
١٢ك ر = ٢ × ٢ × ٣ × ك × ر
٨ر٢ = ٢ × ٢ × ٢ × ر × ر
١٦ر ن = ٢ × ٢ × ٢ × ٢ × ر × ن
إذن (ق. م. أ) لوحيدتي الحد هو ٢ × ٢ × ر = ٤ر,
شاهد حلول جميع الاسئلة
حل أسئلة تدرب وحل المسائل
حلل كل وحيدة حد فيما يأتي تحليلاً تاماً:
١٠) ٩٥س ص٢
٩٥س ص٢ = ٥ × ١٩ × س × ص × ص
١١) -٣٥أ٣ جـ٢
-٣٥أ٣ جـ٢ = - ١ × ٥ × ٧ × أ × أ × أ × جـ × جـ
١٢) ٤٢جـ٣ هـ٣
٤٢جـ٣ هـ٣ = ٢ × ٣ × ٧ × جـ × جـ × جـ × هـ × هـ × هـ
١٣) ٨١ن٥ ب
٨١ن٥ ب = ٣ × ٣ × ٣ × ٣ × ن × ن × ن × ن × ن × ب
١٤) -١٠٠ك٤ ر
-١٠٠ك٤ ر = -١ × ٢ × ٢ × ٥ × ٥ × ك × ك × ك × ك × ر
١٥) ١٢١أ ب جـ٣
١٢١أ ب جـ٣ = ١١ × ١١ × أ × ب × جـ × جـ × جـ
أوجد (ق. م. أ) لكل مجموعة وحيدات حد مما يأتي:
١٦) ٢٥س٣، ٤٥س٤، ٦٥س٢
٢٥س٣ = ٥ × ٥ × س × س × س
٤٥س٤ = ٣ × ٣ × ٥ × س × س × س × س
٦٥س٢ = ٥ × ١٣ × س × س
إذن (ق. م. أ) لوحيدتي الحد هو ٥ × س × س = ٥س٢
١٧) ٢٦ع٢، ٣٢ع، ٤٤ع٤
٢٦ع٢ = ٢ × ١٣ × ع × ع
٣٢ع = ٢ × ٢ × ٢ × ٢ × ٢ × ع
٤٤ع٤ = ٢ × ٢ × ١١ × ع × ع × ع × ع
إذن (ق. م. أ) اوحيدتي الحد هو ٢ع.
١٨) ٣٠جـ هـ٢، ٤٢جـ٢ هـ، ٦٦جـ
٣٠جـ هـ٢ = ٥ × ٢ × ٣ × جـ × هـ × هـ
٤٢جـ٢ هـ = ٢ × ٣ × ٧ × جـ × جـ × هـ
٦٦جـ = ٢ × ٣ × ١١ × جـ
إذن (ق. م. أ) لوحيدتي الحد هو ٢ × ٣ × جـ = ٦جـ
١٩) ١٢ك ر، ٨ر٢، ١٦ر ن
١٢ك ر = ٢ × ٢ × ٣ × ك × ر
٨ر٢ = ٢ × ٢ × ٢ × ر × ر
١٦ر ن = ٢ × ٢ × ٢ × ٢ × ر × ن
إذن (ق. م. أ) لوحيدتي الحد هو ٢ × ٢ × ر = ٤ر,
٢٠) ٤٢أ٢ ب، ٦أ٢، ١٨أ٣
٤٢أ٢ ب = ٢ × ٣ × ٧ × أ × أ × ب
٦أ٢ = ٢ × ٣ × أ × أ
١٨أ٣ = ٢ × ٣ × ٣ × أ × أ × أ
إذن (ق. م. أ) لوحيدتي الحد هو ٢ × ٣ × أ × أ = ٦ أ٢
٢١) ١٥ر٢ ن، ٣٥ن٢، ٧٠ر ن
١٥ر٢ ن = ٣ × ٥ × ر × ر × ن
٣٥ن٢ = ٥ × ٧ × ن × ن
٧٠ر ن = ٢ × ٥ × ٧ × ر × ن
إذن (ق. م. أ) لوحيدتي الحد هو ٥ × ن = ٥ن
٢٢) كعك: يريد حامد وضع العدد نفسه من كل نوع من الكعك في كل كيس، بحيث يحتوي الكيس على أنواع الكعك جميعها ما أكبر عدد ممكن من الأكياس يلزمه؟
٥٤ = ٢ × ٣ × ٣ × ٣
٤٠ = ٢ × ٢ × ٢ × ٥
٣٠ = ٢ × ٣ × ٥
(ق, م, أ) = ٢
كيسان بحيث يحتوي كل كيس على ١٥ بزبده الفستق، ١٠ بالشوفان والزبيب، ٢٧ برقائق الشوكولاتة.
٢٣) هندسة: مساحة مثلث ٢٨ سم، كم يمكن أن يكون طول كل من قاعدته وارتفاعه بالأعداد الكلية؟
- الارتفاع ١ سم والقاعدة ٥٦سم،
- الارتفاع ٢ سم والقاعدة ٢٨ سم،
- الارتفاع ٤ سم والقاعدة ١٤ سم،.
- الارتفاع ٧ سم والقاعدة ٨ سم،
- الارتفاع ٨ سم والقاعدة ٧ سم،
- الارتفاع ١٤ سم والقاعدة ٤ سم،
- الارتفاع ٢٨ سم والقاعدة ٢ سم،
- الارتفاع ٥٦ سم والقاعدة ١ سم,
٢٤) كتب: بكم طريقة تستطيع أسماء تنظيم ٣٦ كتاباً على رفين على الأقل، بحيث يوضع على كل رف العدد نفسه من الكتب، ولا يقل عن ٤؟
- رفان و ١٨، كتاباً،
- ٣ رفوف و١٢ كتاباً،
- ٤ رفوف و ٩ كتب،
- ٦ رفوف و ٦ كتب،
- ٩ رفوف و ٤ كتب,
٢٥) معلبات: بكم طريقة يستطيع سعيد ترتيب ٨٠ علبة على أربعة رفوف على الأقل، بحيث يكون عدد العلب متساوياً على كل رف ولا يقل عن ٥؟
- ٥ علب على ١٦ رفاً، أو
- ٨ علب على ١٠ رفوف، أو
- ١٠ علب على ٨ رفوف، أو
- ١٦ علبة على ٥ رفوف، أو
- ٢٠ علبة على ٤ رفوف.
٢٦) تبرع: اشترى صقر مجموعة اللوازم المدرسية التالية: ٢٠ قلم رصاص، ١٥٠ ورقة ملونة، ١٢٠ ملف أوراق، ويريد وضعها في حزم متماثلة؛ ليتبرع بها لأكبر عدد ممكن من الطلاب، كم حزمة يمكنه عملها؟
٢٠ = ٢ × ٢ × ٥
١٥٠ = ٢ × ٣ × ٥ × ٥
١٢٠ = ٢ × ٣ × ٢ × ٢ × ٥
(ق, م, أ) = ٢ × ٥ = ١٠
١٠ حزم.
تحتوي كل حزمة على قلمين رصاص و١٥ ورقة ملونة و١٢ ملفاً.
٢٧) نظرية الأعداد: العددان التوأمان هما عددان أوليان فرديان متتاليان، أول زوجين منهما هما: ٣، ٥، ٥، ٧. اكتب الأزواج الخمسة التالية لهما.
١١، ١٣، ١٧، ١٩، ٢٩، ٣١، ٤١، ٤٣، ٥٩، ٦١
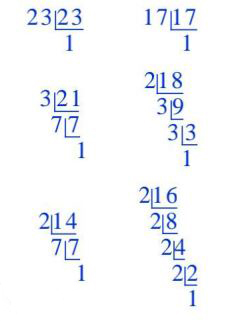
٢٨) تمثيلات متعددة: ستكتشف في هذا السؤال طريقة تحليل عدد إلى عوامله الأولية.
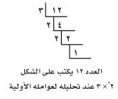
أ) تحليلياً: انسخ مخطط السلم المبين جانباً ٦ مرات، وسجل في الجزء العلوي الأيمن من كل شكل عدداً كلياً، بحيث يكون اثنان منها أوليين.
ب) تحليلياً: اختر عاملاً أولياً لأحد الأعداد، وسجل العامل إلى يسار هذا العدد في الشكل، ثم قسم العددين واكتب الناتج تحت العدد، وكرر الخطوات السابقة حتى يصبح ناتج القسمة ١، وأضف أو أحذف أجزاء من الشكل إذا تطلب الأمر ذلك، ثم كرر هذه العملية مع جميع الأعداد.
متروك للطالب.
جـ) لفظياً: ما التحليل للعوامل الأولية لكل عدد من الأعداد الستة؟
متروك للطالب.
٢٩) تحد: أوجد أصغر زوج من الأعداد يحقق الشروط الآتية: (ق, م, أ) لعددين يساوي ١١، أحدهما زوجي والآخر فردي، وأحدهما ليس من مضاعفات الآخر.
٢٢ (زوجي) = ٢ × ١١
٣٣ (فردي) = ٣ × ١١
ق, م, أ = ١١
أصغر زوج يحقق الشروط هو ٢٢، ٢٣
٣٠) تبرير: المضاعف المشترك الأصغر (م. م. أ) لعددين أو أكثر هو أصغر عدد يكون مضاعف لكل عدد منها، اكتب أوجه الشبه والاختلاف بين (ق. م. أ) و (ق. م. أ) لعددين أو أكثر.
نجد كلاً من (م. م. أ)، (ق. م. أ) باستعمال العوامل الأولية للأعداد: لإيجاد (ق. م. أ) نضرب العوامل الأولية المشتركة بين الأعداد فقط لإيجاد (م. م. أ) نضرب جميع العوامل الأولية,
٣١) تبرير: هل العبارة "القاسم المشترك الأكبر لأي وحيدتي حد لا يساوي ١ أبداً " صحيحة أم خاطئة؟ ادعم إجابتك بمثال أو مثال مضاد.
العبارة خاطئة، (ق. م. أ) لوحيدتي الحد ٩٩س٥ ص١١ ع٣٠، ١٠١ أ ب جـ يساوي ١.
٣٢) تحد: يسمى العددان الصحيحان أو وحيدتا الحد أوليين فيما بينهما، إذا كان (ق. م. أ) لهما هو العدد ١. انقل الجدول المجاور، ثم أكمله لتحدد أزواج وحيدات الحد التي تكون أولية فيما بينهما.
| وحيدة حد | التحليل إلى العوامل الأولية |
| ١٥أ٢ ب جـ٣ | ٣ × ٥ × أ٢ ب جـ٣ |
| ٦ب٣جـ٣ د | ٢ × ٣ × ب٣جـ٣ د |
| ١٢ جـ د٢ ف | ٢٢ × ٣ جـ د٢ ف |
| ٢٢د٣ ف ل٢ | ٢ × ١١ × د٣ ف ل٢ |
| ٣٠ ف٢ ل هـ٢ | ٢ × ٣ × ٥ ف٢ ل هـ٢ |
١٥ أ٢ ب جـ٣، ٢٢ د٣ ف ل٢
٣٣) مسألة مفتوحة: اكتب ثلاث وحيدات حد على أن يكون (ق. م. أ) لها ٦ص٣ فسر إجابتك.
٦ص٣، ١٢ص٤، ١٨ص٥.
٦ هو أكبر عاكل عددي مشترك بين وحدات الحد الثلاث ص٣ أعلى قوة مشتركة لـ ص.
٣٤) اكتب: عرف التحليل إلى العوامل الأولية بكلماتك الخاصة، وفسر كيف تحلل وحيدة الحد إلى عواملها الأولية، وكيف يساعدك هذا التحليل على تحديد (ق. م. أ) لوحيدتي حد أو أكثر.
لتحليل عدد إلى عوامله الأولية نكتب قائمة العوامل الأولية للعدد ويوجد لذلك ثلاث طرق:
- الطريقة الأولى: هي إيجاد العوامل الأولية الصغرى، والاستمرار في قسمة العدد على أعداد أولية صغيرة حتى نوجد جميع الأعداد الأولية ثم كتابة هذه العوامل كحاصل ضرب.
- الطريقة الثانية: يمكن استعمال الرسم الشجري وذلك بالبدء باختيار أي عاملين للعدد، ثم الاستمرار بإيجاد العوامل الأخرى لكل فرع من الشجرة، والانتهاء بالعوامل الأولية, ويمكن وضع دائرة حول العوامل الأولية لمتابعتها.
- الطريقة الثالثة: استعمال مخطط السلم وذلك بالبدء بقسمة العدد على عامل أولي والاستمرار بالقسمة على عوامل أولية للوصول إلى الناتج ١.
٣٥) ما قيمة هـ في المعادلة ٤هـ - ٢٧ = ١٩ + ٢هـ؟
أ) -٤
ب) ٤
جـ) ٢٣
د) ٤٦
٤هـ - ٢٧ = ١٩ + ٢هـ
٤هـ - ٢هـ = ١٩ + ٢٧ = ٤٦
٢هـ = ٤٦
هـ = ٢٣
إذن الاختيار الصحيح: جـ) ٢٣
٣٦) إجابة قصيرة: أوجد ميل المستقيم المار بالنقطتين (٢، ١)، (-٥، ١).
الميل = = (-٣، ٠)
٣٧) ما معادلة المستقيم الذي يوازي المستقيم المبين في الشكل؟
أ) ص = ٢س + ٤
ب) ص = -٢س - ٥
جـ) ص = س -٦
د) ص = - س + ٣
ميل المستقيم في التمثيل البياني = = -٢
حيث الميل =
الميل = معامل س
إذن الإجابة الصحيحة ب) ص = -٢س - ٥

.JPG)
.JPG)

.JPG)
.JPG)
.JPG)